時間因子可加入到雷射引信目標散射回波混沌粒子群最佳化算法中，在算法後期與 K-means 算法進行有效的結合，實驗結果表明該算法能充分利用混沌粒子群算法的全局搜尋能力，並有效改善 K-means 算法依賴初始聚類中心的問題，算法精度得到很大程度提高。
基本介紹
- 中文名：時間因子
- 外文名：Time factor
- 描述：標準粒子群算法公式參數
- 套用：混沌粒子群最佳化算法
- 學科：物理
概念,一種帶自適應飛行時間因子的粒子群算法,自適應飛行時間因子的粒子群算法,數值實驗和結果分析,研究結論,大地震前區域能量場的時間因子異常特徵,能量場時間因子的異常特徵,分析討論,
概念
時間因子在雷射引信目標散射回波的仿真模型中，從標準粒子群最佳化算法的兩個公式可以看出，粒子所處的當前位置是上一次疊代位置與當前速度之和。從物理學角度，只有量綱相同的物理量之間才可以進行數值運算，即位移和位移之間進行相應的計算，速度和速度之間進行運算，所以，標準粒子群算法公式中隱含著時間因子這個參數， 並且這個時間因子通常取固定值1，即在標準粒子群算法中，所有的粒子的飛行時間因子都相同且為1， 顯然這在粒子實際飛行過程中是不可能的。又因飛行時間因子是導致粒子在局部最優解附近來回震盪的一個很重要的因素，實際上粒子在飛行後期過程中會進行局部探索而不斷接近全局最優解， 粒子的飛行時間會越來越短。
一種帶自適應飛行時間因子的粒子群算法
粒子群算法於1995年由Eberhate和Kennedy提出，是一種基於群體的、模擬鳥群社會行為的隨機搜尋過程。在粒子群算法中，種群保持一定數量，群體中每個粒子代表著最佳化問題的一個潛在解，整個群體代表了最佳化問題的若干潛在解。粒子群算法的目的是尋找一個粒子的位置，使得目標函式達到最優。基本粒子群算法存在後期收斂速度慢及容易陷入局部極值的缺點，為了提高算法的收斂速度或收斂精度，許多學者對基本粒子群算法的參數進行不同方式的選擇與最佳化， 提出很多改進方法。1998年，shi等提出帶慣性權重的標準粒子群算法，在此基礎上又有很多學者提出慣性權重自適應改變的PSO算法，如慣性權重隨疊代線性下降、按非線性函式下降、隨著某種評價指標自適應變化。1999年，Clerc提出帶收縮因子的PSO算 法，該算法可以保證PSO算法收斂。2006年，張建科等提出帶飛行時間因子的粒子群算法，給出3種飛行時間因子調整方案。2011年，周喜虎等提出讓飛行時間因子隨著種群多樣性改變的PSO算法。上述方法均或多或少提高了算法收斂速度或收斂精度，但仍然存在高維問題下收斂速度慢或不穩定等問題。
為提高算法的收斂速度和收斂精度，本研究通過引入飛行時間因子，提出一種帶自適應飛行時間因子的粒子群算法，並通過對4種基本函式進行測試，比較了較高維數下AFTPSO算法與其他幾種PSO算法的最佳化性能。
自適應飛行時間因子的粒子群算法
傳統的粒子群算法往往無法兼顧收斂速度和收斂精度，一般在保證收斂速度的情況下，算法容易陷入局部最優。本研究提出的AFTPSO通過控制粒子飛行速度和飛行時間來達到全局搜尋和局部搜尋平衡，以保證算法能夠在較快速度下找到問題的解。
（1）飛行時間因子
上式是基本粒子群算法中粒子的位置更新公式，從物理角度考慮粒子位置改變應加上一個位移， 式中相當於所有粒子飛行時間都為1，顯然，鳥群覓食過程不可能保證每次飛行時間都一樣，而且理論上在覓食初期往往需要大範圍搜尋，飛行時間比較長，而在接近食物的時候，每次飛行時間會縮短，這樣更容易找到食物。基於這種考慮，在式中引入了飛行時間因子，得到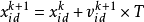
其中，T表示第i個粒子的飛行時間，顯然，基本粒子群算法中T=1。
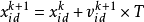
（2）自適應的飛行時間因子
飛行時間隨著粒子的進化而變化，粒子進化程度越高飛行時間應該越小，但考慮到種群多樣性會隨著進化越來越差，導致粒子更易陷入局部最優，此時就需要調整飛行時間來平衡種群的多樣性和進化度，使得粒子在不陷入局部最優情況下，更快收斂到全局最優。本研究在參考其他參數選擇與最佳化對粒子群算法性能影響的情況下，對如何選取飛行時間因子提出了如下方法：
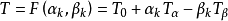
來調節αk和βk這兩個參數對飛行時間因子的影響程度。
數值實驗和結果分析
本研究提出的粒子群算法新增加了飛行時間因子T，T的表達式中包括參數T0，Tα和Tβ，在進行多次實驗之後，發現T0為0.8-1.0時算法效果較好，所以選取T0=0.9。Tα和Tβ可以動態調整，一般較大的Tα會使算法容易跳過最優解陷入振盪狀態，較大的Tβ會使算法容易陷入局部最優，因此適當選取Tα和Tβ的值，對算法的性能提升有較大的影響。經過多次實驗發現，Tα在0.05-0.1取值，Tβ在0.4-0.6取值時，AFTPSO算法的性能較好，在對比實驗中，AFTPSO算法中Tα和Tβ的取值分別為0.08和0.45。根據上述參數設定，各PSO對每個測試函式分別運行20次，測試結果見表1。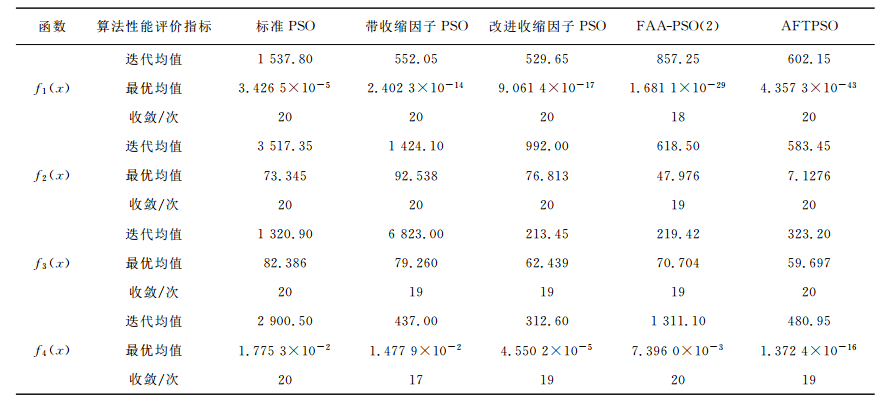
表1 各種粒子群算法對4個測試函式最佳化結果對比表
表1 各種粒子群算法對4個測試函式最佳化結果對比表研究結論
在改進粒子群算法中引入飛行時間因子，並通過考慮種群的多樣性與進化度，動態調整飛行時間因子，以此來平衡算法的全局搜尋和局部搜尋能力，提高了算法的收斂速度和收斂精度。數值實驗表明，該算法的收斂性能明顯優於標準粒子群算法，也優於帶收縮因子的粒子群算法、改進收縮因子的粒子群算法和文獻中提出的改進粒子群算法。本算法中飛行時間因子只是關於種群多樣性與進化度的簡單線性函式，還可以考慮其他非線性函式。另外，隨著粒子群算法研究的深入，可以將一些改進的粒子群算法結合傳統的聚類分析方法進行高維數據聚類分析，進行進一步研究。
大地震前區域能量場的時間因子異常特徵
地震釋放能量是地震活動的基本要素，在一定程度上反映了地殼深部物理力學狀態的變化信息。由於中小地震的發生具有隨機性，因而可將地震活動能量作為隨機場，採用正交函式展開方法分析其時空特徵和變化規律，探索大地震發生前可能的異常信息。筆者套用該方法研究了2008年汶川8.0級地震前震中附近區域的能量場，結果發現，震前能量場的幾個主要典型場的時間因子出現了明顯突升或突降異常變化。筆者以往還曾就此方面開展過一些研究，認為進一步研究地震活動能量場的時空特徵和變化規律，是探索地震預測的一個重要的途徑和方法。
圖1 部分地震前能量場主要典型場時間因子的變化
圖1 部分地震前能量場主要典型場時間因子的變化圖1給出了不同地區的8次地震前4個典型場時間因子的變化曲線，其他地震的時間因子曲線與此相類似。由圖1顯示出，地震發生前幾個主要特徵值所對應的典型場的時間因子出現突升或突降異常變化，與此後發生的強地震有較好的對應關係。
能量場時間因子的異常特徵
通過對30次6級以上地震震例的分析表明，大地震發生前幾個主要特徵值所對應的典型場的時間因子出現突升或突降變化，顯示出與未來強地震有較好的對應關係。筆者認為，能量場時間因子可能是強地震前的異常觀測量和中短期異常指標。典型場的時間因子異常特徵表現為：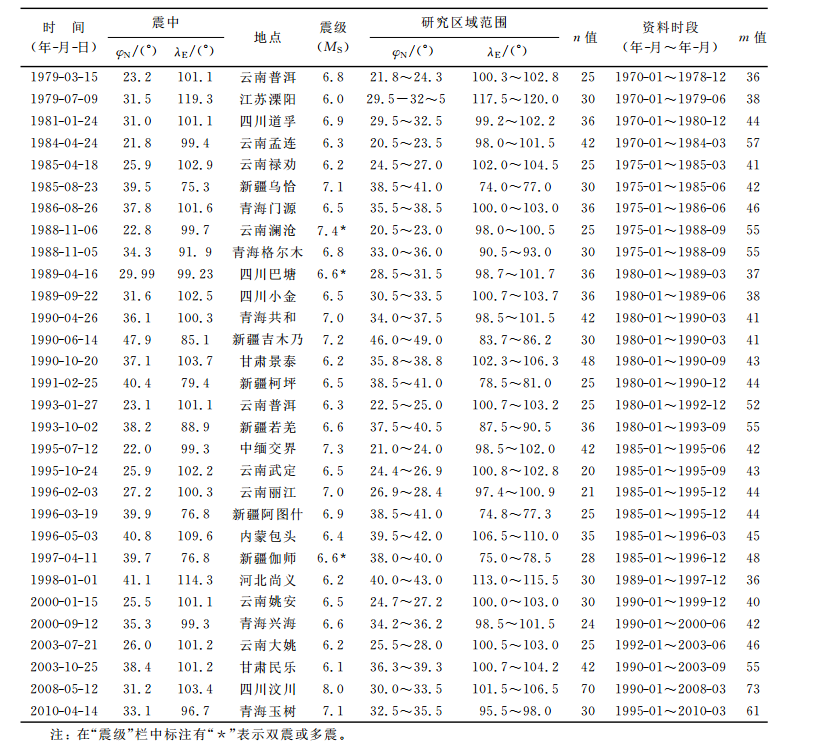
表2 各次地震的研究區域和時段
表2 各次地震的研究區域和時段（1）多數異常具有單點突跳式上升或下降形態，異常具有變化幅度大的特點。由於地震發生是一個隨機脈衝過程，地震能量呈階躍式變化，因此決定了場的時間變化呈突跳式變化特點。一般異常突跳幅度是正常值的幾十倍甚至幾百倍。
（2）大地震前多個典型場的時間因子均發生了異常突升或突降變化，具有場的多分量異常特點。雖然在一些情況下某一典型場的時間因子也會出現突跳變化，但這類變化與區域周圍發生中強地震或地震活動的局部起伏有關，並不具備多個典型場時間因子同時顯示異常的特點。
（3）異常出現的時間Δt一般在震前1～3年，多數小於2年，表現出異常的中短期特點。
（4）有些地震在震前1～3個月出現異常變化，顯示出異常的短臨性質。因此，可以將時間因子異常作為大地震前的中短期或短臨預測指標，並配合其他預測方法進行地震趨勢的判斷。
分析討論
（1）為了進一步說明區域能量場時間因子異常與大地震的關係，以1976年唐山7.8級地震後和2008年汶川8.0級地震前能量場時間因子的變化為例分別加以說明。1976年河北唐山7.8級地震後，震中周圍地震活動相對平靜，期間發生的最大地震為1991年唐山附近一次5.1級地震，並對該地區地震能量場進行了分析。由圖2可見，能量場時間因子沒有出現上述大地震前的異常特徵。該期間曲線的一些突跳變化可能與區域發生的4級多地震活動有關，反映了單個分量的擾動變化，並不具備多分量顯示的特點。
圖2 1980-2010年唐山地震研究區能量場時間因子變化曲線
圖2 1980-2010年唐山地震研究區能量場時間因子變化曲線圖3是1980-2004年汶川研究區域（ 見表2） 能量場時間因子的變化情況。期間該區域內1989年9月發生過小金6.5級地震，圖3中顯示能量場的T1、T2、T4典型場的時間因子出現異常變化。而其他時段時間因子基本上是平穩的，沒有出現具備有震異常特徵的變化。
圖3 1980—2005年汶川研究區能量場時間因子變化曲線
圖3 1980—2005年汶川研究區能量場時間因子變化曲線（2）能量場反映了區域地震活動釋放能量的動態特徵。區域發生的較大地震，特別是一些4級、 5級地震會對時間因子的變化起重大影響，這類變化往往表現為單分量典型場時間因子的變化。
