定義
時序機的定義:時序機是一個5元組,表征為
M=(I,O,Q,N,Z)
其中,I為輸入有限非空集合;O為輸出有限非空集合;Q為時序機狀 態有限非空集合;N為時序機的次態函式,即N:I x Q→Q;Z為時序機的
輸出函式,分兩種情況:
1.若Z:I xQ→O,即輸出是輸入和狀態的函式,該時序機稱為密勒(Mealy)型時序機。
2.若Z:Q→O,即輸出僅僅是狀態的函式, 該時序機稱為莫爾(Moore)型時序機。 時序機可以描述現實世界中與時間、狀態有關的離散時間系統,如日常生活中電話系統、自動售貨機、密碼鎖等。在時序電路中,時序機是一個 有力的工具,甚至一台複雜的計算機都可以由時序機來描述。
狀態表和狀態圖
狀態表和狀態圖是時序機的兩種表述形式。狀態表是用表格的方式來 描述時序機的輸入與狀態轉換關係;狀態圖則是用圖解的方式描述上述關 系。狀態圖更加直觀,狀態表適合於電腦程式化處理。實際上,狀態圖和 狀態表是等價的,可以互相轉換。
下面通過簡單的例子來說明狀態表和狀態圖的具體形式。
例如設計一個1101序列檢測器。
方法如下:該電路有一個輸入端 X 和一個輸出端 Z。在輸入端 X 加上 0/1 信號 序列,當信號序列中出現“101”時,Z 為“l”,否則 Z 為“0”。例如,在 X 上加 上如下信號序列,則檢測器的輸出序列應為:
X:010101101Z:000100001
確定狀態表的過程如下: 首先假設檢測器有一個初始狀態A。若輸入的第l個信號是“1”,它是“101”序列的第1個元素,應該把這個情況記憶下來,檢測器進人狀態B,檢測器輸出為“0”;若輸入的第1個信號是“0”,它不是“101”序列的第1個元素, 不必把這個情況記下來,檢測器仍停留在狀態A,檢測器輸出為“0”。
若電路處於B態(即檢測器已經接收了“101”序列的第1個元素),輸入 信號是“0”,它是被測序列的第2個元素,檢測器應把這個情況記錄下來,並 進人狀態C,同時檢測器的輸出仍應為“0”;若輸入信號是“l”,它不是被測 序列的第2個元素,而仍相當於是第1個元素,所以電路仍停留在狀態B,電 路輸出為“0”。
若電路處於 C態,輸入信號是“1”,它是被測序列的第 3個元素,這時 檢測器已檢出序列“101”,電路輸出為“1”,檢測器把第3個元素記錄下來後, 進入狀態D;若輸入信號是“0”,它不是被測序列的第3個元素,此時電路不 但輸出為“0”,而且還將“報廢”以前已接收的第1、第2個元素“10”,使電路回 到狀態A。
若電路處於D態,輸入信號為“1”,它是第 2個被測序列的第1個元素, 檢測器應把它記下來,電路進入B態;若輸入為“0”,它不是第2個被測序列 的第1個元素,電路應進入A態,等待接收第2個被測序列的第1個元素,輸出 為“0”。
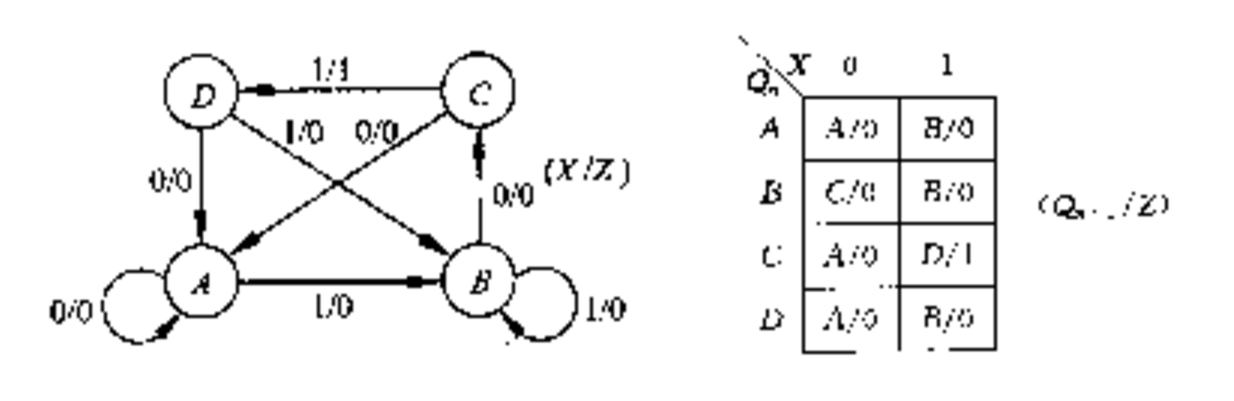
根據以上描述,可知該檢測器有四個原始狀態,它的狀態圖和狀態表如圖所示。
狀態圖由以下元素組成:圓圈代表狀態,每個狀態賦予不同標識,如A、B、C等;狀態轉換用箭頭表示,箭頭尾部是當前狀態(稱為現態,用Q表 示),箭頭指向下一個狀態(稱為次態,用Q(n+1)表示);引起狀態變化的輸 入條件標註在箭頭弧線的旁邊。
狀態表則是狀態圖的表格表示形式。把輸入和現態寫在表格的側面, 表格中填入變化後的次態,就構成了相應的狀態表。狀態表也和狀態圖一樣, 反映出了狀態變化關係。
一般形式
狀態表和狀態圖只要已知其中的一個,就可以求出另一個。在實際套用中,往往將二者結合起來使用。下面給出時序機狀態表、狀態圖的一般形式。
設輸入集合I為I1、I2~In,狀態集合Q為Q1、Q2~Qk,則Mealy機的狀態 表和狀態圖一般形式如下;Moore機的狀態表和狀態圖一般形式如下。
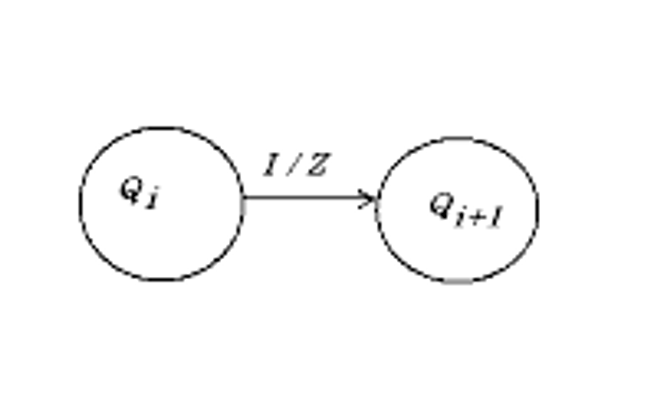
Mealy機
Mealy機的狀態表和狀態圖
I
Q
| I1
| ~
| In
|
Q1
| Qk
| N(Q1,I1)/Z(Q1,I1)
| N(Qk,Ik)/Z(Qk,Ik)
| ~
| N(Q1,In)/Z(Q1,In)
| N(Qk,In)/Z(Qk,In
|
I
Q
| I1
| ~
| In
|
Q1
| Qk
| N(Q1,I1)/Z(Q1,I1)
| N(Qk,Ik)/Z(Qk,Ik)
| ~
| N(Q1,In)/Z(Q1,In)
| N(Qk,In)/Z(Qk,In)
|
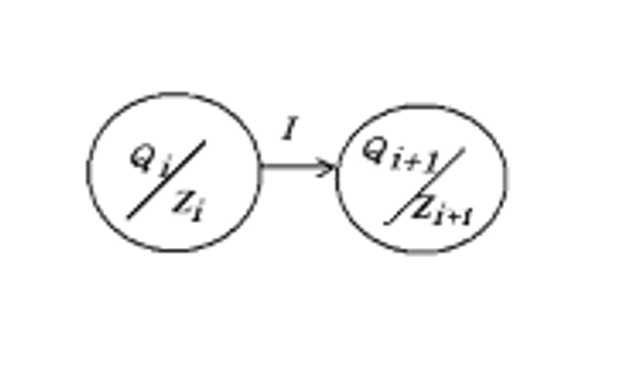
Moore機
Moore機的狀態表和狀態圖
Q1
| Qk
| N(Q1,I1)/Z(Q1)
| N(Qk,Ik)/Z(Qk)
| ~
| N(Q1,In)/Z(Q1,In)
| N(Qk,In)/Z(Qk,In)
| Z(Q1)
| Z(Qk)
|
Q1
| Qk
| N(Q1,I1)/Z(Q1)
| N(Qk,Ik)/Z(Qk)
| ~
| N(Q1,In)/Z(Q1,In)
| N(Qk,In)/Z(Qk,In)
| Z(Q1)
| Z(Qk)
|