基本介紹
- 中文名:旋轉法
- 外文名:rotation method
- 學科:數學
- 分類:垂直軸、平行軸、一般位置軸旋轉
- 套用:點、直線、平面的旋轉
- 目的:使空間幾何處在有利於解題的位置
背景
分類
 圖1
圖1點的旋轉
 圖2
圖2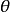
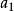
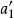
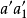
 圖3
圖3直線的旋轉
 圖4
圖4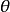
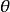
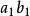
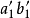
平面的旋轉


 圖1
圖1 圖2
圖2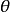
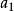
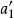
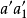
 圖3
圖3 圖4
圖4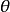
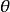
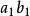
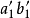

旋轉法是正投影變換的一種方法,它保持投影面不動,將空間幾何元素繞某一軸線旋轉,使它對投影面處在有利於解題的位置。旋轉法可分為垂直軸旋轉、平行軸旋轉和一般...
通過旋轉圖形使旋轉後的圖形與原來的圖形建立起某些聯繫,即通過圖形位置的變化,把條件不甚明顯的量之間的關係轉化為明顯的量的關係,以利於探索出證題的途徑,這種...
是使每個因子上具有最高載荷變數數最小,可簡化對因子解釋的旋轉法。在主成分分析中,用到正交旋轉法,假設各因素相關。假設提取出來的公共因素各不相關,是因素分析...
迫近最大方差斜交旋轉法是在因素分析中旋轉負荷矩陣的一種方法。旋轉法使得因子負荷量更易於解釋,其目的在於改變每個變數在各因子的負荷量的大小。旋轉方法有兩種,...
電漿旋轉法是使高溫下產生的鈾電漿在電磁場中作高速旋轉,在離心力場作用下,質量較大的鈾同位素電漿在徑向方向上逐漸加濃。這種旋轉電漿裝置好像是...
最常用的方法是最大方差正交旋轉法(Varimax)。進行因子旋轉,就是要使因子載荷矩陣中因子載荷的平方值向0和1兩個方向分化,使大的載荷更大,小的載荷更小。因子...
釋文:具體操作又包括如下3種方法:①旋轉針法:將礦物碎屑粘在旋轉針尖上,轉動旋轉針,使其結晶軸平行下偏光振動方向,即可測得主折射率值;②破壞法:硬度大的礦物(...
這種剛體繞固定點的純慣性運動可用分析法或幾何法求解。①分析法 可用雅可比橢圓...剛體繞慣性主軸的運動最為簡單,這種純慣性運動可以使旋轉不變地保持下去,稱為...
整脊療法,又稱“脊住(定點)旋轉復位法”,是以分筋彈撥、按壓疏理等整復手法 整脊療法脊柱穴位及對應器官 作用於脊椎背膂,以促進督脈氣血和暢,使病椎恢復正常,...
6―1更換投影面法 6―2垂軸旋轉法 6―3平軸旋轉法 第七章 平面體 7―1稜柱和稜錐 7―2平面體表面上的點 7―3平面體的截斷 7―4兩平面體相貫 第八章...
換面法的變換規律是:點的新投影到新投影軸的距離等於點的被替換投影到被替換軸的距離。②旋轉法:保持投影面不動,讓空間形體繞某條軸線旋轉到需要的位置,求出新...
10.3 因子旋轉10.3.1 方差最大正交旋轉法的基本原理10.3.2 方差最大正交旋轉法的計算方法10.4 因子得分10.4.1 湯姆生因子得分10.4.2 綜合因子得分...
主成分分析法因子旋轉 在對社會調查數據進行分析時,除了把相關的問題綜合成因子並保留大的因子,研究者往往還需要對因子與測度項之間的關係進行檢驗,以確保每一個...
所謂樹根樁就是在套管導向下用旋轉方法鑽進(鑽孔直徑100一300mm),穿過原有建築物的基礎進入地基土中至設計高程,清孔後下放鋼筋(鋼筋數量視樁孔直徑而定),再用...
4.3 旋轉法第5章 立體5.1 平面立體5.2 曲面立體5.3 平面與立體表面相交5.4 立體與立體相交5.5 組合體第6章 軸測投影圖6.1 軸測投影圖的基本知識...
