通過旋轉圖形使旋轉後的圖形與原來的圖形建立起某些聯繫,即通過圖形位置的變化,把條件不甚明顯的量之間的關係轉化為明顯的量的關係,以利於探索出證題的途徑,這種方法就叫做旋轉法。旋轉法雖然是處理幾何問題的一種重要思考方法,但是在運用旋轉法時要具體問題具體分析,要以使所證問題簡便為準則。
基本介紹
- 中文名:旋轉法作圖
- 外文名:construction by rotation
- 所屬學科:數學
- 所屬問題:平面幾何(尺規作圖)
- 簡介:作圖題解的一種方法
基本介紹,例題解析,
基本介紹
旋轉法作圖(construction by rotation)是作圖題解的一種方法,有些作圖題,需要將某些幾何元素或圖形繞某一定點旋轉適當角度,以使已知圖形與所求圖形發生聯繫,從而發現作圖途徑。
 圖1
圖1例如,已知三條平行線求作一個正三角形,使三個頂點分別在這三條平行線上,其思路要點是:假設△ABC是正三角形,且頂點A,B,C分別在直線a,b,c上,作AD⊥b,將△ABD繞A點逆時針旋轉60°後置於△ACD′的位置,此時,點D′可以確定,從而C點亦可確定,再作∠BAC=60°,B點又可確定,故符合條件的正三角形可以作出(如圖1),若不考慮正△ABC的具體位置,而只考慮三個頂點分別在三條平行線上,則此題只有一解。
例題解析
【例1】已知:E是正方形ABCD的BC邊上任意一點,∠EAD的平分線AF與CD交於F,求證:DF=AE-BF。
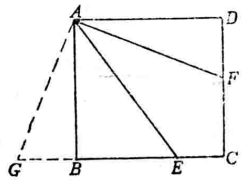 圖2
圖2證明:如圖2所示。
以A為中心,把△ADF旋轉90°,使∠ADF轉到△ABG的位置。
∵AD=AB,
∴AD與AB重合。
又∠D=∠ABG=90°,
顯然BG與BC在一條直線上。
∵∠GAB=∠DAF=∠FAE,
∴∠GAE=∠BAF=∠AFD=∠AGB,
∴AE=GB+BE=DF+ BE,
即DF=AE-BF。
 圖3
圖3證明: 如圖3所示。以F為中心,把△FDC按順時針方向旋轉60°,則FC變到FB位置。
∵CD//AB且CD=AB,∠EBA=60°,
∴CD變到BE位置,FD= FE,
且 ∠DFE= 60°,
∴△DEF是正三角形。
以上旋轉都是以三角形為基礎進行旋轉的。根據具體問題,還可能以正方形或其它一些任意圖形為基礎進行旋轉;而旋轉的度數可能是90°、60° 或其它任意度數;因此,採用這種方法證題時,要具體問題具體分析。

