翻折法作圖(construction by reflection)是解作圖題的一種常用方法，一些作圖題可以通過固定圖形中適當的一條直線或一點，將圖形翻折，利用圖形的對稱性使某些幾何元素移位，以尋求到作圖的途徑和方法，從而作出所求圖形。
基本介紹
- 中文名：翻折法作圖
- 外文名：construction by reflection
- 所屬學科：數學
- 所屬問題：平面幾何(尺規作圖)
- 簡介：解作圖題的一種常用方法
基本介紹,舉例分析,用中心對稱法解題,用軸對稱法解題,
基本介紹
翻折法作圖（construction by reflection）也稱對稱法作圖，就是利用國中幾何課中學到的軸對稱和中心對稱的知識去解幾何題目，常收巧妙、簡捷、明快之效，我們把這種方法稱之為翻折法或對稱法。具體的說，就是：假設圖形已經作出，如將某定點或定線段以一已知直線(或線段)為對稱軸，而得出它的對稱點或線段。仍可具有原來的點或線毆所應滿足的某些條件。這樣：往往可將原問題化為比較簡易的問題。
例如，已知直線XY同側的兩點A，B，在直線XY上求作一點P，使PA+PB為最短(如圖).簡要分析如下：
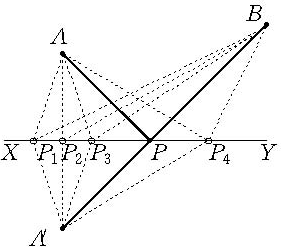圖1若將點A從直線XY所劃分的上半平面翻折到下半平面的點A′，則斜線(或垂線)AP，AP1，AP2，AP3，…的長分別與對應斜線(或垂線)A′P，A′P1，A′P2，A′P3，…的長相等，因此折線APB，AP1B，AP2B，AP3B，…之長分別與對應折線(或線段)A′PB，A′P1B，A′P2B，A′P3B，…之長相等.於是使PA+PB最短的問題便化為使PA′+PB最短的問題.根據兩點之線段比兩點間折線短的原理知，線段A′B與直線XY的交點便是所求的點.
本題恆有解，包括直線AB與XY互相垂直的情形在內，那時AB的垂足即所求的點。
舉例分析
用中心對稱法解題
把一個圖形繞某一點旋轉180°，便得到這個圖形關於這個點的中心對稱圖形，因此中心對稱法實際是一種旋轉法(轉180°)， 以下只舉一個例子。
例1 如圖，△ABC中，邊BC上的兩點E，F把BC三等分，BM是AC邊上的中線，AE、AF分BM為x、y、z三部分，求x：y：z。
圖2解:以M為中心，作△ABC的中心對稱圖形△CB'A，則E、E'和F、F'都是關於點M為對稱中心的對稱點。
∴E'C//AE，F'C// AF，
由此可得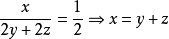 
， ①
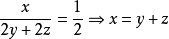
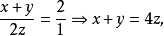
由①得x-y=z， ③
②+③，得，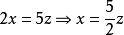
，
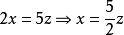
②-③，得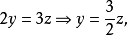
∴
.
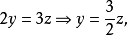
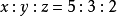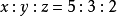
用軸對稱法解題
有些書籍只將軸對稱法又稱翻折法，當幾何問題條件不太集中，已知求證之間聯繫不大時，有時用翻折法可把條件相對集中，容易發現新的解題途徑，下面按不同的對稱軸介紹幾種常見的翻折類型。
1.以角平分線為軸
例2 已知等腰直角三角形ABC中，∠A=90°，∠B的平分線交AC於D，過C作BD的垂線交BD的延長線於E。
圖3求證：BD= 2CE，證明：以角平分線BE為軸，作△BCE的軸對稱圖形△BFE，則C. E，F共線，且CE=EF，即CF= 2CE。
∵∠1=22.5°，
而∠ACF=90°-∠2-∠ACB=90°-22.5°-45°=22.5°，
又AB= AC，
∴△ABD≌△ACF，
∴BD=CF=2CE。
2.以高線為軸
例3已知銳角△ABC，AH是BC邊上的高，若AB+ BH= HC，求證:∠B=2∠C。
圖4證明:如圖，以A為軸，作△ABH的對稱圖形△AB'H，則AB'= AB，HB' =BH，
∵AB+BH =HC，
∴AB'+ HB'=HC，
∴AB'= B'C，
∴∠C=∠B'AC，
而∠B=∠AB'B=∠B'AC+∠C，
∴∠B=2∠C.
3. 以直徑為軸
例4如圖，AB是⊙O的直徑，弦CD與AB交於P，∠CPB=45°，⊙O的半徑為1，求證: PC2+ PD2=2。
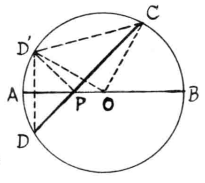圖5證明：以AB為軸，作PD的對稱圖形PD'，連結DD'，OD'、OC、CD'，則有
PD= PD'，∠CDD'=45°，∠D'PC = 2∠CDD'= 90°，
∴∠COD'= 2∠CDD'= 90°，
∴PC2+ PD2=PC2+ PD'2= CD'2= OC2+OD'2=2.
4. 折線問題
常用來解決折線的最小值問題，下面舉一個和折線角度相關的問題。
例5 已知直線AB的同側有兩點P、Q (且PQ不垂直於AB)，在AB上確定一點C，使∠PCA=2∠QCB。
圖6作法:如圖，以AB為軸作點Q的對稱點Q'，以Q'圓心，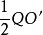
為半徑作⊙O'，過P作⊙O'的切線PD與AB交於C，則點C就是要 'Q'求的點。
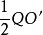
證明:∵∠PCA=
∠BCD, CE是⊙O'的切線，
∴∠ ECQ'=∠DCQ'，
又∵∠QCE=∠Q'CE，
∴∠PCA=2∠Q'CE= 2∠QCB.
