格拉斯曼流形(Stiefel manifold)是通過坐標空間的原點的所有 n 維平面的集合,這可以視為一個商空間。
基本介紹
- 中文名:施蒂費爾流形
- 外文名:Stiefel manifold
- 適用範圍:數理科學
簡介,性質,商空間,
簡介
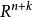
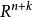
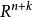
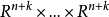

性質
格拉斯曼流形有一個標準映射
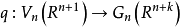
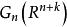


格拉斯曼流形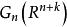 是nk維緊光滑流形。
是nk維緊光滑流形。
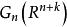
商空間
(quotient space)
線上性代數中,一個向量空間V被一個子空間N的商是將N“坍塌”為零得到的向量空間,所得的空間稱為商空間,記作V/N(讀作V模N)。






格拉斯曼流形(Stiefel manifold)是通過坐標空間的原點的所有 n 維平面的集合,這可以視為一個商空間。
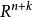
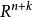
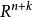
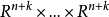

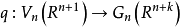
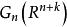


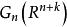






格拉斯曼流形(Stiefel manifold)是通過坐標空間的原點的所有 n 維平面的集合,這可以視為一個商空間。中文名 施蒂費爾流形 外文名 Stiefel manifold 適用範圍 ...
施蒂費爾-惠特尼類(Stiefel-Whitney classes)是向量叢的底空間的上同調類。...... 微分流形M的切叢T(M)的施蒂費爾-惠特尼類稱為M的施蒂費爾-惠特尼類,記為ωi...
(2)示性類 施蒂費爾只考慮微分流形的切叢的示性類,而惠特尼考慮的要廣得多,他考慮自由球叢(E,B,P)的底空間B也可以是任意局部有限的單純複合形.他把示性...
惠特尼對偶定理(Whitney duality theorem)是微分流形的切叢與餘切叢的施蒂費爾-惠特尼類的關係。...
的一個 n 標架是 中線性無關向量的一個 n 元組, 中的所有 n 標架的全體構成 n重直積 的一個開子集,稱其為施蒂費爾流形 。...
1936年瑞士數學家施蒂費爾考慮以微分流形的每一點為原點的有限個線性獨立向量場,引入流形的微分同胚不變數。1937年美國數學家惠特尼把流形及以其上每一點為原點的...
惠特尼乘積定理(Whitney product theorem)屬於惠特尼與吳文俊,由惠特尼乘積定理可定義施蒂費爾-惠特尼類。...
