方程術是一種解線性方程組的消元算法,出自《九章算術》。
方程術(Fangchengshu)中國古算法.指《九章算術》中提出的一種解線性方程組的消元法.今舉例如下:第八章“方程”第一題:“今有上禾三秉,中禾二秉,下禾一秉,實三十九斗;上禾二秉,中禾三秉,下禾一秉,實三十四斗;上禾一秉,中禾二秉,下禾三秉,實二十六斗.問上、中、下禾實一秉各幾何?”依術文列出方程如下:

其消元過程如下:
1.“以右行上禾遍乘中行而以直除”,即以右行上禾3遍乘中行各數,然後從中行中累減右行兩次,得
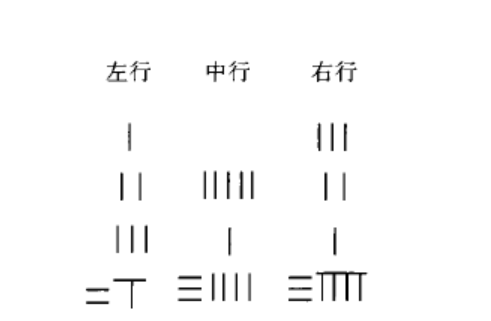
2.“又乘其次,亦以直除”,意即以右行上禾3遍乘左行各數,然後從左行內減去右行,得
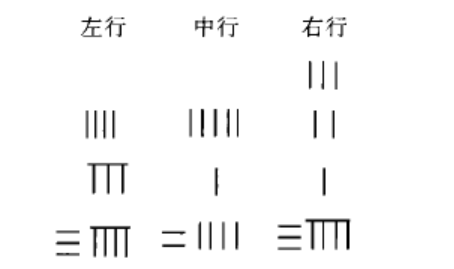
3.“然以中行中禾不盡者遍乘左行而以直除”,即以中行5遍乘左行,然後從左行內累減中行,得
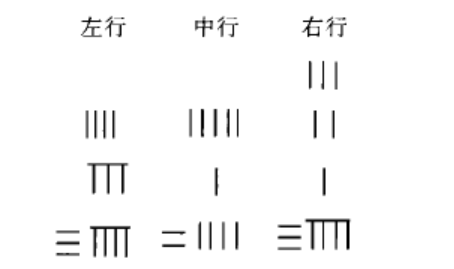
4.“左方下禾不盡者,上為法,下為買,買即下禾之實."99為下禾之實.
5.“求中禾,以法乘中行下實,而除下禾之實.余如中禾秉數而一,即中禾之實.”中禾之實為

其中“直除法”就是兩行對應數字相減,以達到消去其中一個數字的目的.劉徽的解釋是“令少行減多行,反覆相減,則頭位必先盡”.
