基本介紹
- 中文名:斯圖爾特定理
- 外文名:Stewart's theorem
- 表達式:mb^2+nc^2=a(d^2+mn).
- 提出者:Matthew Stewart
- 提出時間:1746年
- 套用學科:數學
- 適用領域範圍:平面幾何
發展簡史,定理內容,證明,套用,
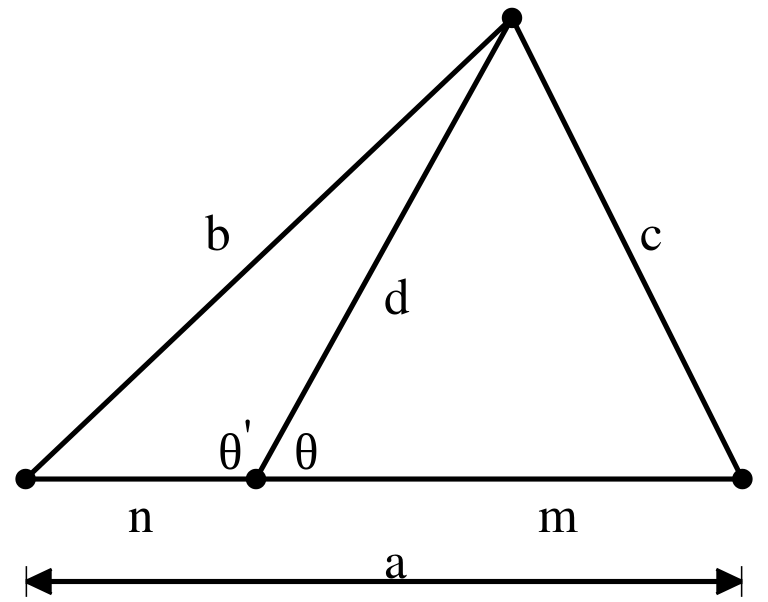
在幾何學中,斯圖爾特定理(Stewart's theorem)給出了邊長和三角形中的cevian長度之間的關係,它的名字是為了紀念蘇格蘭數學家馬修斯圖爾特(Matthew Stewart),他在1746年...
該定理可以證明是斯圖爾特定理的一個特例,或者可以用向量證明。以下是使用餘弦定律證明。圖2.Apollonius定理的證明 設三角形具有邊 ,其中線 被繪製到a側。設 是由...
常見定理有勾股定理,歐拉定理,斯圖爾特定理等。 中文名 幾何 外文名 geometry 分類 數學 提出 李煥蘭 功能 研究空間結構及性質 ...
18. 斯圖爾特定理(27) 19. 函式關係(28) 20. 等腰三角形的斯圖爾特定理1(30) 21. 等腰三角形的斯圖爾特定理2(31) 22. 內心1(32) 23. 內心2(34) 24. ...
