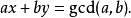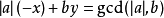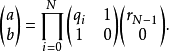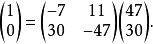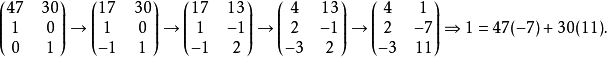簡介
擴展歐幾里得算法(英語:Extended Euclidean algorithm)是
歐幾里得算法(又叫輾轉相除法)的擴展。已知整數a、b,擴展歐幾里得算法可以在求得a、b的
最大公約數的同時,能找到整數x、y(其中一個很可能是負數),使它們滿足貝祖等式
如果a是負數,可以把問題轉化成
,然後令x'=(-x)。
通常談到
最大公約數時,我們都會提到一個非常基本的事實:
給予二個整數a、b,必存在整數x、y使得ax + by = gcd(a,b)。
有兩個數a,b,對它們進行輾轉相除法,可得它們的最大公約數——這是眾所周知的。然後,收集輾轉相除法中產生的式子,倒回去,可以得到ax+by=gcd(a,b)的整數解。
例子
用類似
輾轉相除法,求二元一次不定方程47x+30y=1的整數解。
實現
def ext_euclid(a, b): if b == 0: return 1, 0, a else: x, y, q = ext_euclid(b, a % b) # q = gcd(a, b) = gcd(b, a%b) x, y = y, (x - (a // b) * y) return x, y, q
int gcdEx(int a,int b,int*x,int*y){ if(b==0) { *x=1,*y=0 ; return a ; } else { int r=gcdEx(b,a%b,x,y); /* r = GCD(a, b) = GCD(b, a%b) */ int t=*x ; *x=*y ; *y=t-a/b**y ; return r ; }}