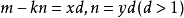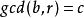基本介紹
- 中文名:輾轉相除法
- 外文名:Euclidean algorithm
- 別稱:歐幾里德算法
- 用途:求最大公約數
- 歸屬學科:數學
- 出現書目:《幾何原本》
基本原理


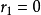



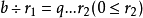
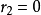





證明






算法描述

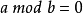
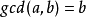
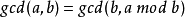
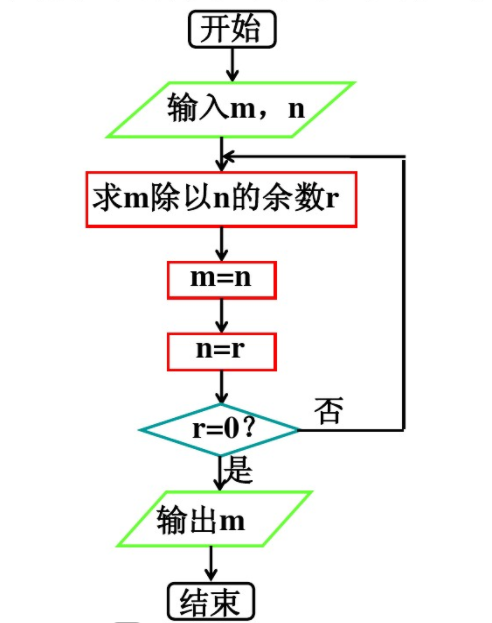
function gcd(a,b) {if b< >0 return gcd(b,a mod b);else return a;}示例
例1
a | b | a mod b |
123456 | 7890 | 5106 |
7890 | 5106 | 2784 |
5106 | 2784 | 2322 |
2784 | 2322 | 462 |
2322 | 462 | 12 |
462 | 12 | 6 |
12 | 6 | 0 |
例2














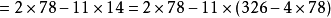
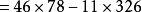




代碼實現
c語言
int GCD(int a,int b){ return b==0?a:GCD(b,a%b);}C++語言實現
#include<iostream>using namespace std;int a , b , a1 , b2 , l;int gcd(int x , int y){ if(!y) return x;else return gcd(y , x%y); }int main(){cout << "請輸入兩個正整數,計算它們的最大公約數" << endl ;int a , b , ans;cin >> a >> b;if(a > b)ans = gcd(a , b);else ans = gcd(b , a);cout << ans;return 0;}C#語言實現
static int sucDivison(int m, int n) /*除法*/{ int remainder = 0; if (m % n == 0) { return n; } else { do { remainder = m % n; m = n; n = remainder; } while (remainder > 0); } if (n == 0) { return m; } return n; }Basic實現
INPUT m,n DO r=m MOD nm=nn=rLOOP UNTIL r=0PRINT mEND
Pascal實現
function gcd(a,b:integer):integer;begin if b=0 then gcd:=a else gcd:=gcd(b,a mod b);end;
Java 實現
public static int gcd(int m, int n) { while (true) { if ((m = m % n) == 0) return n; if ((n = n % m) == 0) return m;}}Python實現
#遞歸解決最大公約數問題def gcd(x , y): if y == 0 return x else gcd(y, x%y) x = int(input('請輸入第一個數字:'))y = int(input('請輸入第二個數字:'))print('%d 和 %d 的最大公約數為:' %(x,y),gcd(x,y))#非遞歸def gcd(x, y): while y: x, y = y, x%y return x