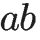模反元素

如果兩個正整數a和n互質，那么一定可以找到整數b，使得 ab-1 被n整除，或者說ab被n除的餘數是1。這時，b就叫做a的“模反元素”。

基本介紹

• 中文名：模反元素
• 外文名：modulo multiplicative inverse
• 同義詞：模逆元素

如果兩個正整數a和n互質，那么一定可以找到整數b，使得 ab-1 被n整除，或者說ab被n除的餘數是1。

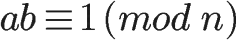
這時，b就叫做a對模數n的“模反元素”。比如，3和11互質，那么3的模反元素就是4，因為 (3 × 4)-1 可以被11整除。顯然，模反元素不止一個， 4加減11的整數倍都是3的模反元素 {…,-18,-7,4,15,26,…}，即如果b是a的模反元素，則 b+kn 都是a的模反元素。

歐拉定理可以用來證明模反元素必然存在。

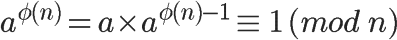
可以看到，a的 φ(n)-1 次方，就是a對模數n的模反元素。