二叉排序樹(排序二叉樹):定義,查找,插入刪除,插入算法,刪除結點,性能分析,最佳

二叉排序樹

排序二叉樹一般指本詞條

二叉排序樹（Binary Sort Tree），又稱二叉查找樹（Binary Search Tree），亦稱二叉搜尋樹。是數據結構中的一類。在一般情況下，查詢效率比鍊表結構要高。

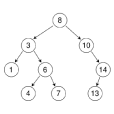
基本介紹

中文名：二叉排序樹
外文名：Binary Sort Tree
別名：二叉查找樹、二叉搜尋樹
別稱外文名：Binary Search Tree

定義,查找,插入刪除,插入算法,刪除結點,性能分析,最佳化,

定義

一棵空樹，或者是具有下列性質的二叉樹：

（1）若左子樹不空，則左子樹上所有結點的值均小於它的根結點的值；

（2）若右子樹不空，則右子樹上所有結點的值均大於它的根結點的值；

（3）左、右子樹也分別為二叉排序樹；

【注】：以上的三種定義在不同的數據結構教材中均有不同的定義方式但是都是正確的在開發時需要根據不同的需求進行選擇

【注2】：沒有鍵值相等的結點。

查找

步驟：若根結點的關鍵字值等於查找的關鍵字，成功。

二叉樹

否則，若小於根結點的關鍵字值，遞歸查左子樹。

若大於根結點的關鍵字值，遞歸查右子樹。

若子樹為空，查找不成功。

平均情況分析（在成功查找兩種的情況下）：

在一般情況下，設 P（n，i）為它的左子樹的結點個數為 i 時的平均查找長度。結點個數為 n = 6 且 i = 3; 則 P（n,i）= P（6, 3） = [ 1+ ( P(3) + 1) * 3 + ( P(2) + 1) * 2 ] / 6= [ 1+ ( 5/3 + 1) * 3 + ( 3/2 + 1) * 2 ] / 6

注意：這裡 P(3)、P(2) 是具有 3 個結點、2 個結點的二叉分類樹的平均查找長度。在一般情況，P（i）為具有 i 個結點二叉分類樹的平均查找長度。平均查找長度= 每個結點的深度的總和 / 總結點數

（二叉樹圖中應為左子樹P(3)，右子樹P(2)）

P(3) = （1+2+2）/ 3 = 5/3

P(2) = （1+2）/ 2 = 3/2∴ P（n,i）= [ 1+ ( P(i) + 1) * i + ( P(n-i-1) + 1) * (n-i-1) ] / n

∴ P（n）=

P（n,i）/ n <= 2(1+I/n)lnn

因為 2(1+I/n)lnn≈1.38logn 故P(n)=O(logn)

插入刪除

與次優二叉樹相對，二叉排序樹是一種動態樹表。其特點是：樹的結構通常不是一次生成的，而是在查找過程中，當樹中不存在關鍵字等於給定值的結點時再進行插入。新插入的結點一定是一個新添加的葉子結點，並且是查找不成功時查找路徑上訪問的最後一個結點的左孩子或右孩子結點。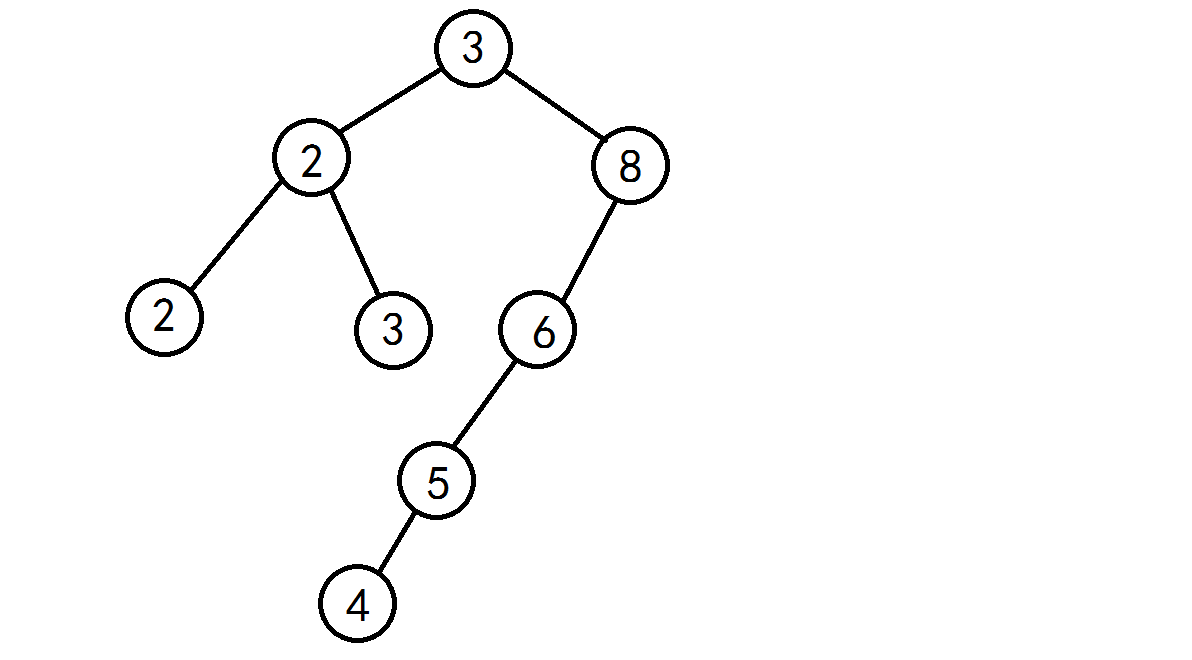

二叉樹

插入算法

首先執行查找算法，找出被插結點的雙親結點。

判斷被插結點是其雙親結點的左、右兒子。將被插結點作為葉子結點插入。

若二叉樹為空。則首先單獨生成根結點。

注意：新插入的結點總是葉子結點。

struct BiTree {
    int data;
    BiTree *lchild;
    BiTree *rchild;
};
//在二叉排序樹中插入查找關鍵字key
BiTree* InsertBST(BiTree *t,int key)
{
    if (t == NULL)
    {
        t = new BiTree();
        t->lchild = t->rchild = NULL;
        t->data = key;
        return t;
    }
    if (key < t->data)
        t->lchild = InsertBST(t->lchild, key);
    else
        t->rchild = InsertBST(t->rchild, key);
    return t;
}
//n個數據在數組d中，tree為二叉排序樹根
BiTree* CreateBiTree(BiTree *tree, int d[], int n)
{
    for (int i = 0; i < n; i++)
        tree = InsertBST(tree, d[i]);
}

刪除結點

在二叉排序樹刪去一個結點，分三種情況討論：

若*p結點為葉子結點，即PL(左子樹)和PR(右子樹)均為空樹。由於刪去葉子結點不破壞整棵樹的結構，則可以直接刪除此子結點。

若*p結點只有左子樹PL或右子樹PR，此時只要令PL或PR直接成為其雙親結點*f的左子樹（當*p是左子樹）或右子樹（當*p是右子樹）即可，作此修改也不破壞二叉排序樹的特性。

若*p結點的左子樹和右子樹均不空。在刪去*p之後，為保持其它元素之間的相對位置不變，可按中序遍歷保持有序進行調整，可以有兩種做法：其一是令*p的左子樹為*f的左/右(依*p是*f的左子樹還是右子樹而定)子樹，*s為*p左子樹的最右下的結點，而*p的右子樹為*s的右子樹；其二是令*p的直接前驅（或直接後繼）替代*p，然後再從二叉排序樹中刪去它的直接前驅（或直接後繼），即讓*p的左子樹的最右節點（或右子樹的最左節點）*s替代*p，再將原*s的左子樹根節點（或右子樹根節點）替代原*s。在二叉排序樹上刪除一個結點的算法如下：

C++代碼

#define Status bool
Status Delete(BiTree*);//必須先聲明
Status DeleteBST(BiTree &TParent,BiTree &T, KeyType key)//若二叉排序樹T中存在關鍵字等於key的數據元素時，則刪除該數據
                                    //元素，並返回TRUE；否則返回FALSE
{
    if(!T)//不存在關鍵字等於key的數據元素
        return false;
    else
    {
        if(key == T->data.key)//找到關鍵字等於key的數據元素                   
            return Delete(TParent, T);
        else if(key < T->data.key)
            return DeleteBST(T, T->lchild,key);
        else
            return DeleteBST(T, T->rchild,key);
    }
    return true;
}
Status Delete(BiTree& fp , BiTree&p)//從二叉排序樹中刪除結點p，並重接它的左或右子樹
{
    if(!p->rchild)//右子樹空則只需重接它的左子樹
    {
        fp->lchild = p->lchild;
        delete(p);
     }
    else if(!p->lchild)//左子樹空只需重接它的右子樹
    {
        fp->rchild = p->rchild;
        delete(p);
    }
    else//左右子樹均不空
    {
            q=p;
            fp->lchild = p->lchild;
            s=p->lchild;//轉左
        while(s->rchild)//然後向右到盡頭
        {
           q=s;
            s=s->rchild;
        } //此時q是s的父結點
        s->rchild=p->rchild; //將s的左子樹作為q的右子樹
        delete(p);
     }
    return true;
}

Java代碼
/**
*方法名稱：delete()
*方法描述：刪除結點
*@param採用遞歸的方式進行刪除
*@returnString
*@Exception
*/
private void deleteNode(BinarySortTree p)
{
    //TODOAuto-generatedmethodstub
    if(p!=null)
    {
        //如果結點有左子樹
        /*1。若p有左子樹，找到其左子樹的最右邊的葉子結點r，用該葉子結點r來替代p，把r的左孩子
        作為r的雙親的右孩子。
        2。若p沒有左子樹，直接用p的右孩子取代它。
        */
        if(p.lChild!=null)
        {
            BinarySortTree r=p.lChild;
            BinarySortTree prev=p.lChild;
                while(r.rChild!=null)
               {
                    prev=r;
                    r=r.rChild;
                }
                p.data=r.data;
            //若r不是p的左子樹,p的左子樹不變，r的左子樹作為r的雙親結點的右孩子結點
            if(prev!=r)
            {
                prev.rChild=r.lChild;
             }
            else
            {
             //若r是p的左子樹，則p的左子樹指向r的左子樹
            p.lChild=r.lChild;
            }
        }
        else
        {
            p=p.rChild;
        }
    }
}

性能分析

每個結點的C(i)為該結點的層次數。最壞情況下，當先後插入的關鍵字有序時，構成的二叉排序樹蛻變為單支樹，樹的深度為其平均查找長度(n+1)/2(和順序查找相同），最好的情況是二叉排序樹的形態和折半查找的判定樹相同，其平均查找長度和log 2 (n)成正比。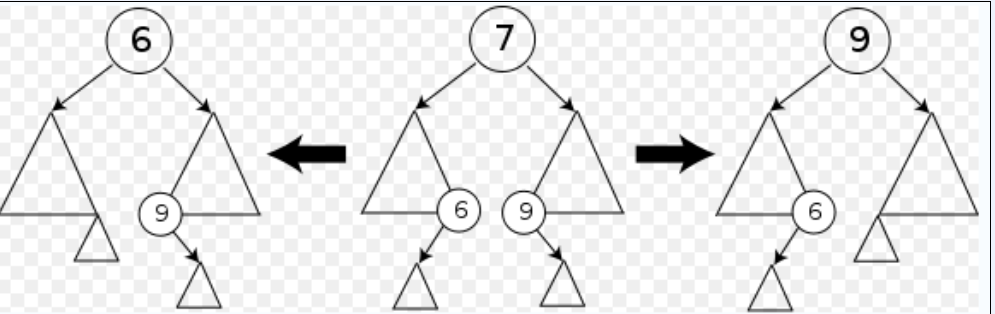

性能分析