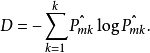分類樹是指在遙感圖像分類中，根據地面景物的總體規律及內在聯繫而建立的一種樹狀結構的框架。在用於分類的決策樹，即分類樹(classification tree)中，劃分的優劣用不純性度量(impurity measure)定量分析。一個劃分是純的，如果對於所有分支，劃分後選擇相同分支的所有實例都屬於相同的類。
基本介紹
- 中文名：分類樹
- 外文名：classification trees
- 所屬學科：數學（統計學）
- 相關概念：回歸樹，基尼係數，交叉熵等
基礎知識,基本介紹,分裂標準,分類錯誤率,基尼係數,交叉熵,
基礎知識
下圖是一個簡單的確定汽車駕駛員風險的決策樹(decision tree)，使用這個樹時，先考慮駕駛員的年齡。如果小於18歲，則考慮是否開紅車，如果是，則認為該駕駛員是高風險的，否則是低風險的；如果年齡大於18歲，則考慮是否酗酒，如果是，則高風險，否則為低風險，當然，這個決策樹僅僅是描述性的，比較簡單。
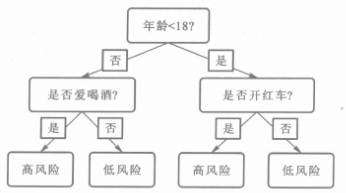圖1這個決策樹像一棵倒長的樹(當然也可以橫著放)，變數年齡所在的節點稱為根節點(root node)，而底部的四個節點稱為葉節點(leaf node)或終節點(terminal node)。這個樹也稱為分類樹(classification tree)，因為其目的是要把一個觀測劃分為“高風險“或“低風險”每個葉節點都是因變數的取值，而除了葉節點外的其他節點都是自變數。對於這個決策樹，只要輸人關於某司機的這幾個變數的值，就立刻得到該司機相關的風險分類，
還有一種決策樹是回歸樹(regression tree)，其根節點為連續的因變數在這個分叉上的平均取值，分類樹和回歸樹合起來也叫做CART(elassification andregression tree)，上面的描述性決策樹是二分的( binary split)，即每個非葉節點(non-leaf node)剛好有兩個叉。決策樹也可有多分叉的(multi-way split) 。決策樹的節點上的變數可能是各種形式的(連續、離散、有序、分類變數等)，一個變數也可以重複出現在不同的節點，一個節點前面的節點稱為其父節點(母節點或父母節點，parent node)，而該節點為前面節點的子節點( 女節點或子女節點，child node)，並列的節點也叫兄弟節點(姊妹節點，sibling node)。上面的例子是一棵現成的樹，它不是隨便畫的，而是根據數據做出來的。
和經典回歸不同，決策樹不需要對總體進行分布的假定，而且，決策樹對於預測很容易解釋，這是其優點，此外，決策樹很容易計算，但有必要設定不使其過分生長的停止規則或者修剪方法，決策樹的一個缺點是每次分叉只和前一次分叉有關，而且並不考慮對以後的影響。因此，每個節點都依賴於前面的節點。如果開始的劃分不同，結果也可能很不一樣，目前有些人在研究分叉時考慮未來，但由於可能導致強度很大的計算，還沒有見之於實際套用階段。
基本介紹
決策樹是一種從無次序、無規則的樣本數據集中推理出決策樹表示形式的分類規則方法。採用自上向下的遞歸方式，在決策樹的內部節點進行屬性值的比較，並根據不同屬性值判斷從該節點向下分，在決策樹的葉結點得到結論。因此，從根節點到葉節點的一條路徑就對應一條規則，整棵決策樹就對應著一組表達式規則。比較典型的決策樹算法是由Breiman於1984 年提出的分類回歸樹(CART,Classification and簡稱為CART分類樹)，並不斷得到改進，現已在統計和Regression Trees，數據挖掘領域中普遍使用。它提供了一種非參數判別多數據層之間的統計關係，通過構建二叉樹達到預測目的，採用一種二分遞歸分割的技術，將當前的樣本集分為兩個子樣本集，使得生成的決策樹的每個非葉子節點都有兩個分支，其核心就是通過對由測試變數和目標變數構成的訓練數據集的循環二分形成二叉樹形式的決策樹結構。CART分類樹包含兩個基本思想：第一是將練樣本進行遞歸地劃分自變數空間進行建樹的想法；第二是用驗證數據進行剪枝。
分裂標準
分類錯誤率
構建分類樹和回歸樹在方法上大體相似，同回歸樹一樣，用遞歸二元分裂法構建分類樹。然而不同之處在於，殘差平方和(RSS)不能作為二元分裂的標準，因此用分類錯誤率(Classification Error Rate)來替代殘差平方和。由於我們的目的是用該區域內訓練樣本最可能發生的類別來推斷觀測值的歸屬，因此分類錯誤率指的就是訓練樣本沒有被分入最可能發生的類別的比率，即:
基尼係數
基尼係數(Gini Index)是對組間總方差的度量，當趨於0或趨於1時，基尼係數值很小。對此，通常把基尼係數作為對節點純度的度量——基尼係數小代表節點包含了來自某一單獨類別的主要的觀測值。
交叉熵
由於
，所以,
。同樣當趨於0或趨於1時，交叉熵(Cross-entropy)很小，接近於0。因此，同基尼係數一樣，交叉熵的值很小時代表節點的純度高。事實上，基尼係數和交叉熵在數值上是十分相似的。
因為基尼係數和交叉熵相比於分類錯誤率對節點的純度更敏感，所以在構建分類樹的時候，通常使用基尼係數或是交叉熵來評價某一分裂的質量。然而在修剪分類樹時，儘管三種方法都可以使用，但是如果修剪分類樹的目的是提高預測精度，那么分類錯誤率的指標更好。
