托姆分類定理(Thom classification theorem )是突變理論的核心定理。一個局部函式f:U→R,U⊂R,稱為一個奇點,若f(0)=0,∂f/∂xi(0)=0 (i=1,2,…,n)。
基本介紹
- 中文名:托姆分類定理
- 外文名:Thom classification theorem
- 領域:數學
- 學科:突變理論
- 提出:托姆
- 相關:局部微分同胚
概念
托姆分類定理(Thom classification theorem )是突變理論的核心定理。一個局部函式f:U→R,U⊂R,稱為一個奇點,若f(0)=0,∂f/∂xi(0)=0 (i=1,2,…,n)。

托姆分類定理(Thom classification theorem )是突變理論的核心定理。一個局部函式f:U→R,U⊂Rn,稱為一個奇點,若f(0)=0,∂f/∂xi(0)=0 (i=1,2,…,n)。概念托姆分類定...
托姆定理(Thom theorem)是關於托姆空間的同倫群同構於定向配邊群的定理。簡介 托姆定理是關於托姆空間的同倫群同構於定向配邊群的定理。該定理斷言:設k>n+1,萬有托姆空間的同倫群 標準同構於定向配邊群Ωₙ。類似地,與未定向萬有...
托姆創立了配邊理論,他指出任何兩個流形屬於同一類的充分必要條件,從而完成了流形的粗分類的工作,然後他又對每一類找出一個代表,有了這些代表,任何一個流形就屬於某一個代表的類了。在托姆之前,數學家也曾考慮類似的問題。蘇聯數學...
托姆同構定理 托姆同構定理是示性類理論中的一個定理。簡介 托姆同構定理是向量叢上同調群之間存在同構的定理。定義 設R為交換環,μ∈ 為n平面叢 的托姆類。定義 為 。則 為同構。
托姆橫截性定理 托姆橫截性定理(Thom transversality theo-em)微分拓撲學的重要定理.它也是動力系統理論研究的重要工具.它表明流形之間具有橫截性的映射是“足夠普遍”的.設M,N都是C'流形,f:M}N是C'映射,AcN是N的C'子流形。
從1949年起托姆研究微分流形之間映射的奇點理論,1954年證明了橫截性定理。1956年開始研究流形特別是歐氏空間之間函式(芽)的奇點分類問題,得出一系列基本結果。這些結果形成突變論的數學基礎。1966年後他還對葉狀結構的奇點理論及動力系統的...
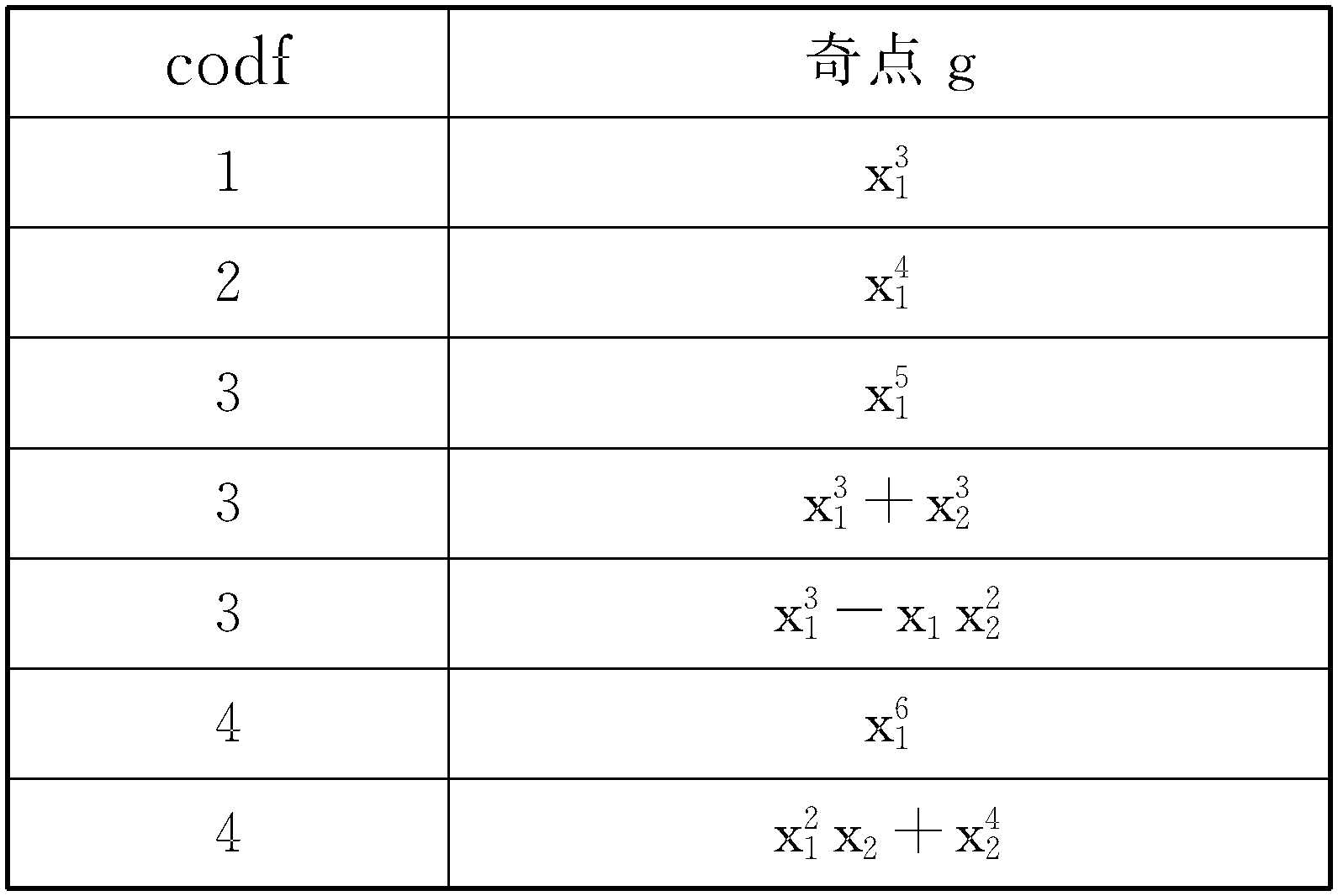
托姆(R.Thom)在分類定理與開折理論的基礎上創立的7種基本的突變模型是突變理論的主要內容。從數學上來說,它們的勢函式即奇點分類定理中的奇點的萬有開折;從模型的意義來說,它們是外部控制參數在1與4之間的穩定靜模型必等價於其中...
除了通過各數學分支的間接的影響外,拓撲學的概念和方法對物理學(如液晶結構缺陷的分類)、化學(如分子的拓撲構形)、生物學(如DNA的環繞、拓撲異構酶)都有直接的套用。初等實例 除去七橋問題,四色問題,歐拉定理等,拓撲學中還有...
托姆基本定理 其中 為旋轉群的托姆譜。結構定理 是Q上多項式環,即每 維 各有一個生成元,這生成元為復射影空間的定向配邊類 。1960年,米爾諾證明 沒有p分量,p為任意奇素數。同年,沃爾證明 的2分量中不含4階元素。設 為...
