基本介紹
- 中文名:截柱體
- 外文名:truncated cylinder
- 所屬領域:立體幾何(多面體)
- 相關概念:直截面、準線、母線等
基本介紹
定義一



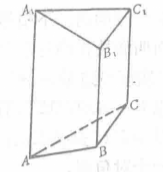
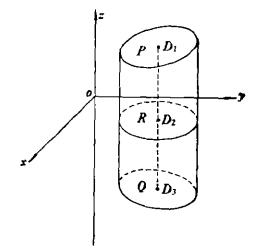
定義二
斜截柱體的體積和側面積計算
定理1














推理1
推理2
定理2
套用舉例
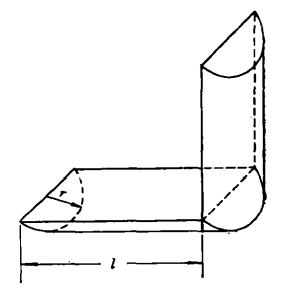






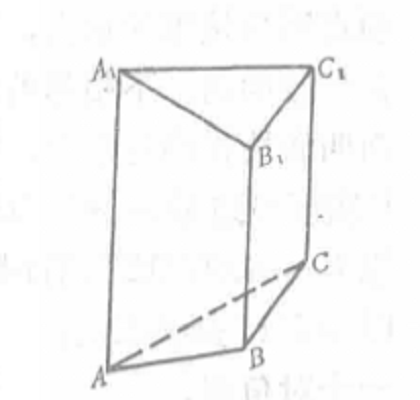


























截柱體(truncated cylinder)是一種與柱體有關的幾何體,用一個與柱體所有母線都相交的平面去截柱體,所得的兩個幾何體都稱為原柱體的截柱體。當截面平行於底面時,截柱體亦是柱體。當截面不平行於底面時,截柱體稱為...
考慮等截面柱體,取z軸沿柱體縱軸方向,柱體兩端在xy面內受扭矩T的作用。在非圓形截面柱體的扭轉問題中,截面不僅產生轉動,而且產生翹曲。下面介紹求解這類問題的半逆解法和薄膜比擬方法。半逆解法 由於單位柱長上截面的相對轉角θ較小,...
優選地,所述的第一本體為中空柱體。進一步地,所述柱體的橫截面沿周向形成封閉的一圈。優選地,所述的第一本體包括具有兩個側端的基部,所述基部的兩個側端之間形成開口,基部的兩個側端向內或向外延伸形成一對側邊部,一對所述...
中截面(mid-section)是指與底面平行,且與兩底面等距離的平面截幾何體所得的截面。稜柱的中截面面積等於稜柱的底面積,稜錐的中截面面積等於稜錐底面積的四分之一。基本介紹 中截面(midsection)是一種特殊的截面,指在有兩平行底面(...
楔體是一種特殊的擬柱體,將一個三稜柱(直三稜柱或斜三稜柱)用一個與三棱相交的截面(直截面或斜截面)去截開,所得的幾何體稱為楔體。它是一種擬柱體,下底面為梯形或平行四邊形,上底面是與下底面的平行邊平行的線段。圖1...
而當方柱處於湍流邊界層中,上述雙穩態現象基本消失,展向渦主要以卡門渦街形式出現,此時柱體脈動升力與阻力均遠大於均勻流中的對應值,即湍流邊界層有消除對稱展向渦的趨勢。本項目還通過風洞實驗系統的研究了圓形、方形等典型截面有限長...
斜圓柱(oblique circular cylinder)是底面為圓的斜柱體,是柱體的一種。表面積 圓柱的全面積是刻畫圓柱表面積大小的一個數量及其計算公式。直圓柱的側面積與底面積的和為它的全面積。如果直圓柱的底面半徑為r,高為h,那么它的全面積...
常見的十一面體有錐體和柱體、部分的詹森多面體和半正多面體,此處的半正多面體並非阿基米德立體,而是正九角柱。其他十一面體還有九角柱、十角錐、正五角錐反角柱的對偶、雙對稱十一面體等多面體,其中雙對稱十一面體可以密鋪空間。截半...
對一個小截面積的土壤柱體,如測得降雨量和進出土柱的水量,蒸發量可以作為餘量求得。農業試驗站設定的土壤蒸發器就利用這個原理。水文單位所設的水量平衡場,就取一個小面積的場地,觀測水量平衡若干分量,通過土柱水量平衡法來計算未...
牛頓-辛普森公式是一種適應面較廣的求積公式。這個公式不僅適用於作為擬柱體的稜柱、稜錐和稜台,而且適用於不是擬柱體的圓柱、圓錐、圓台和球檯,甚至像橢球體等。簡介 一個幾何體被垂直於其高(或平行於其底)的平面所截,如果截面...
常見的十五面體有錐體和柱體、部分的詹森多面體、法列士立體和半正多面體,此處的半正多面體並非阿基米德立體,而是正十三角柱。 十五面體是指具有十五個面的多面體。在十五面體中,有1個是詹森多面體,它們分別為:雙五角錐柱。在十一面...
物種名稱 朱魯賽疊層石 生存地點 --- 地質層位 --- 辨認要決 --- 物種種類 --- 介紹 基本層通常被柱邊所截。不具側壁。可具長而向下彎曲的檐或連線橋。通常柱體表面有一包裹柱體的薄膜。
過截角超無限邊形鑲嵌是一種雙曲面鑲嵌,由正方形和超無限邊形構成,是歐氏鑲嵌,截角無限階二邊形鑲嵌在羅氏幾何中的一個類比。該幾何圖形也可以視為是一種“發散”的柱體,由於其可以類比自無限角柱,是指底面是無限邊形的柱體,...
