愛爾蘭全利用度等待系統(Erlangfull aailabilitywaitingsystem)指A.K.愛爾蘭提出的容量有限全利用度線束,按等待(或叫排隊)方式工作的一種數學模型。
基本介紹
- 中文名:愛爾蘭全利用度等待系統
- 外文名:Erlangfull aailabilitywaitingsystem
- 套用學科:通信
相關概念
數學模型
 圖1愛爾蘭全利用度等待系統模型
圖1愛爾蘭全利用度等待系統模型套用
附
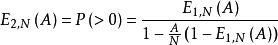
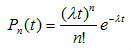
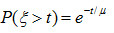
愛爾蘭全利用度等待系統(Erlangfull aailabilitywaitingsystem)指A.K.愛爾蘭提出的容量有限全利用度線束,按等待(或叫排隊)方式工作的一種數學模型。
 圖1愛爾蘭全利用度等待系統模型
圖1愛爾蘭全利用度等待系統模型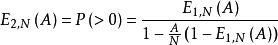
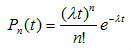
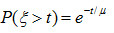
愛爾蘭全利用度等待系統(Erlangfull aailabilitywaitingsystem)指A.K.愛爾蘭提出的容量有限全利用度線束,按等待(或叫排隊)方式工作的一種數學模型。...
關於愛爾蘭全利用度等待系統,已給出計算系統狀態機率分布和呼叫等待時間機率分布的公式,其中包括著名的第二愛爾蘭公式(愛爾蘭公式C)。而且還給出計算呼叫的平均等待時...
隨機服務系統理論的目的在於通過研究系統的特性,合理地處理這個矛盾,並研究出系統的最佳化問題。(2)愛爾蘭全利用度等待系統愛爾蘭全利用度等待系統指A.K.愛爾蘭提出的...
第一愛爾蘭公式(first Erlang formula)指A K.愛爾蘭給出的用於計算無限負載源全利用度損失系統呼損的公式,也稱愛爾蘭呼損公式。實際套用中要求負載源數遠大於線束容量...
隨機服務系統理論,是通過對服務對象到來及服務時間的統計研究,得出這些數量指標(等待時間、排隊長度、忙期長短等)的統計規律,然後根據這些規律來改進服務系統的結構或...
貝克特受存在主義影響,創作了包括《等待戈多》在內的一系列表現現代社會荒誕、...的圓桌騎士的傳說,特別是特里斯丹同綺瑟戀愛的故事,實是後來不列顛系統騎士傳奇的...
“愛爾蘭”(愛爾蘭語:Éire),宣布愛為主權、獨立、民主的國家,仍留在大英國協...愛爾蘭的公眾交通系統既安全又效率高,也比較經濟。公汽、長途汽車和火車是愛爾蘭...
第二愛爾蘭公式(second Erlang formula)是愛爾蘭全利用度等待系統的一個重要公式,用以計算用戶呼叫需要等待的機率。...
愛爾蘭語和不列顛群島其他凱爾特語言一樣,有系統的“頭音交替”音變。 愛爾蘭語的詞形變化是現存各[凱爾特]語言中最複雜的:動詞有人稱、數、時、式、態(主動、...
1909年,丹麥學者A.K愛爾蘭(AgnerKrarupErlang,1878-1929)發表了他的第一篇話務...20世紀30年代,C.D.克羅米林(C.DCrommelin)發表的全利用度等待系統的理論,解決...
克羅米林分布曲線(Crommelin distributioncurves)指根據克羅全利用度等待系統理論公式繪製的一些供工程計算使用的曲線。...
只是在愛爾蘭分布情況下(見無限負載源全利用度損失系統),三種算法的值是相等的。呼損率呼損率與接通率的區別 呼損率與接通率是兩個不同的概念。後者指的是在一定...
