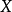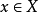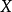強收斂是指測度網(或列)依範數(能量)的收斂。關於點列的收斂性包括兩種:強收斂和弱收斂,並且它們之間存在著這樣的關係:強收斂必定弱收斂,但弱收斂不一定強收斂。
基本介紹
- 中文名:強收斂
- 外文名:strong convergence
- 相關概念:弱收斂、弱*收斂、一致收斂
- 性質:強極限若存在,則極限值唯一
- 類型:點列的強收斂、運算元列的強收斂
- 套用學科:實變函式與泛函分析
定義
點列的強收斂
點列的弱收斂




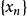

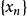


X與其共軛空間中運算元列的收斂性
運算元列的強收斂


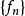

運算元列的弱*收斂




運算元列的弱收斂




X與Y空間中運算元列的收斂性
運算元列的一致收斂




運算元列的強收斂





運算元列的弱收斂