強擬凸域

如果Ω在∂Ω上的每一點都是強擬凸的，就稱Ω是強擬凸域。域的強擬凸性與域的定義函式的選取無關。

基本介紹

• 中文名：強擬凸域
• 外文名：strictly function of a domain
• 適用範圍：數理科學

簡介

設Ω是Cⁿ中的域，Ω在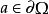處具有C²邊界，φ是Ω在a處的局部定義函式。如果對滿足

的(ξ₁,ξ₂,...,ξ_n)∈Cⁿ，有。如果等號僅當ξ=0時才成立，則稱Ω在a處是強擬凸的。如果Ω在∂Ω上的每一點都是強擬凸的，就稱Ω是強擬凸域。

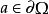
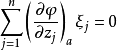
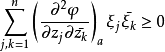
實例

例如：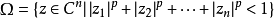

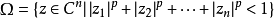
當p=2時，Ω是強擬凸域；

當p≠2時，Ω是擬凸域。

性質

由於域的定義函式不是唯一的，故定義的域的強擬凸性表面上依賴於域的定義函式的選取，事實上，可以證明域的強擬凸性與域的定義函式的選取無關。