弗雷歇定理

弗雷歇定理是關於L²[a,b]空間有界線性泛函一般形式的定理。

基本介紹

• 中文名：弗雷歇定理
• 外文名：Frechet theorem
• 適用範圍：數理科學

定義

弗雷歇定理是關於L²[a,b]空間有界線性泛函一般形式的定理。

若Φ(f)是L²[a,b]上的有界線性泛函，則存在惟一的g(x)∈L²[a,b]，使得Φ(f)=(f,g)對任意f(x)∈L²[a,b]都成立。

提出者背景

弗雷歇（Fréchet，Maurice-René），法國數學家，1878 年 9月2日生於馬利尼，1973年6月4日卒於巴黎。

1910 ～ 1919年任普瓦捷大學力學教授 ，1920年任斯特拉斯堡大學高等微積分學教授。1928年起執教於巴黎大學，先後任機率論講師、一般數學教授、微積分學教授和機率論教授。弗雷歇首次提出抽象空間的定義，奠定了抽象空間的理論。他對數學分析和機率論也有貢獻。

線性有界泛函

若f:D⊂X→^滿足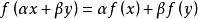，則稱f為線性；

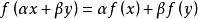
若∀x∈D，|f(x)|≤M||x||，則稱f有界。