弓高

弓高是指組成弓形的弧的中點到組成弓形的弦的垂線段。

（注意：弓高是指一條“垂線段”而不是這條垂線段的長）

如圖，在弧AB與弦AB組成的弓形（實線部分）中，M為弧AB的中點，過點M作MH⊥AB交AB於點H，則垂線段MH為弓形AB的高，即弓形AB的弓高。

基本介紹

• 中文名：弓高
• 外文名：arch's height
• 領域：數學

定義

弓高是指組成弓形的弧的中點到組成弓形的弦的垂線段。

性質

一、唯一性：弓形只有一條唯一確定的弓高。

證明：根據弓高的定義，因為弧有唯一確定的中點，且過直線外一點有且只有一條直線與已知直線垂直，故從弧的中點引弦的垂線段也是唯一確定的。

二、弓高是組成弓形的弧上所有點到弦的垂線段中最長的。

證明：設弓形AB，弧AB上一動點P，及弦∠APB為定值α，△ABP的面積為S，底邊AB上的高為PH。

由正弦定理得： ，又

∴ ，其中 α和AB長為定值，即 。

由弦長定理（弦長積定理）得，當PA=PB時， 達到最大值,即當P為弧AB的中點時,PH達到最大值。

根據弓高的定義可知，此時PH即為弓高。故原命題得證。

三、弓高所在的直線經過弓形所在的圓的圓心。

證明：如圖，MH是弓形AB的弓高。連結MA,MB。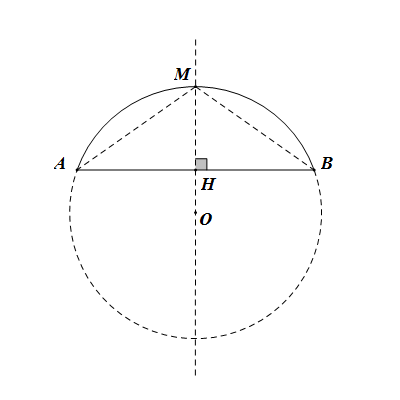

∵M是弧AB的中點，

∴弧AM=弧BM，

∴AM=BM，

∵MH⊥AB，

∴AH=BH，

由垂徑定理的逆定理可得：

直線MH經過弓形AB所在圓的圓心。

四、優弧弓的弓高大於弓形所在圓的半徑，劣弧弓的弓高小於弓形所在圓的半徑，半圓弓的弓高等於弓形所在圓的半徑。

長度計算公式

【公式一】在弓形中，設弓形所在圓的半徑為 ，組成弓形的弦長為 ，組成弓形的弦的弦心距為 ，

則有： ，且弓高 （當弓形為優弧弓時）或 （當弓形為劣弧弓時）。

當然，若弓形為半圓弓，直接可得

推導：同上述題設，如圖弓形中，設⊙O的半徑為r，AB=a，MH=h。

延長MH，由弓高的性質三可得MH過圓心O，連結OA。

由垂徑定理得 ，

由勾股定理得：

由弓高的性質四可以得到高 （當弓形為優弧弓時）或 （當弓形為劣弧弓時）。

【公式二】若已知弓形的弧所對圓心角為θ，則：

再根據情況運用公式計算即可。

（或已知弧所對圓周角也可直接用圓周角的餘弦值和正切值計算）

套用

可用與實際問題當中。

一、在排水管中，已知排水管的規格，可以將排水管中的水擬作弓形，利用水深、水位線長（即弓形的弦長）等計算一些數據（如弓高、水流量、流速），以更好地進行運水輸水排水等的管理。

二、有些橋樑或大門的形狀為拱形，且為其中特殊的一種——弓形。此時可以根據弓形的性質和弓高的計算方法測量計算橋樑、大門等的一些數據。