庫利－圖基快速傅立葉變換算法

庫利－圖基快速傅立葉變換算法（Cooley-Tukey算法）是最常見的快速傅立葉變換算法。這一方法以分治法為策略遞歸地將長度為N = N1N2的DFT分解為長度分別為N1和N2的兩個較短序列的DFT，以及與旋轉因子的複數乘法。

基本介紹

• 中文名：庫利－圖基快速傅立葉變換算法
• 外文名：Cooley-Tukey

簡介

這種方法以及FFT的基本思路在1965年J. W. Cooley和J. W. Tukey合作發表An algorithm for the machine calculation of complex Fourier series之後開始為人所知。但後來發現，實際上這兩位作者只是重新發明了高斯在1805年就已經提出的算法（此算法在歷史上數次以各種形式被再次提出）。

庫利－圖基快速傅立葉變換算法是將序列長為N的DFT分區為兩個長為N/2的子序列的DFT，因此這一套用只適用於序列長度為2的冪的DFT計算，即基2-FFT。實際上，如同高斯和庫利與圖基都指出的那樣，庫利－圖基算法也可以用於序列長度N為任意因數分解形式的DFT，即混合基FFT，而且還可以套用於其他諸如分裂基FFT等變種。儘管庫利－圖基算法的基本思路是採用遞歸的方法進行計算，大多數傳統的算法實現都將顯示的遞歸算法改寫為非遞歸的形式。另外，因為庫利－圖基算法是將DFT分解為較小長度的多個DFT，因此它可以同任一種其他的DFT算法聯合使用。

複雜度

離散傅立葉變換的複雜度為 （可引用大O符號）。快速傅立葉變換的複雜度為，分析可見下方架構圖部分，級數為而每一級的複雜度為 ，故複雜度為。

時域-頻域抽取法

在FFT算法中，針對輸入做不同方式的分組會造成輸出順序上的不同。如果我們使用時域抽取（Decimation-in-time），那么輸入的順序將會是比特反轉排列（bit-reversed order），輸出將會依序排列。但若我們採取的是頻域抽取（Decimation-in-frequency），那么輸出與輸出順序的情況將會完全相反，變為依序排列的輸入與比特反轉排列的輸出。

DIF FFT

時域抽取法

我們可以將DFT公式中的項目在時域上重新分組，這樣就叫做時域抽取（Decimation-in-time），在這裡將會被代換為旋轉因子（twiddle factor）。

在這邊我們要注意的是，我們所替換的G[k]與H[k]具有周期性：

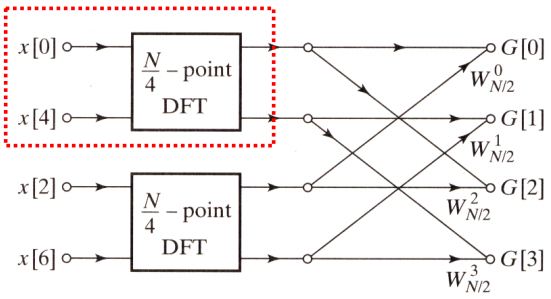
上述的推導可以劃成下面的推導圖：

推導圖

劃紅框處所示的點DFT架構如圖1所示：

圖1 DFT架構圖1

劃紅框處所示的 點DFT架構如圖2所示：

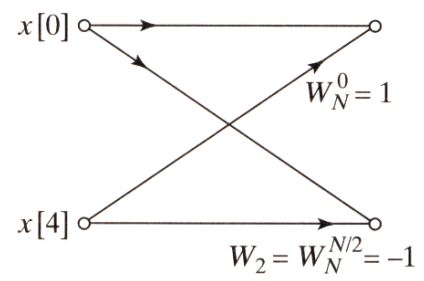
圖2 DFT架構圖2

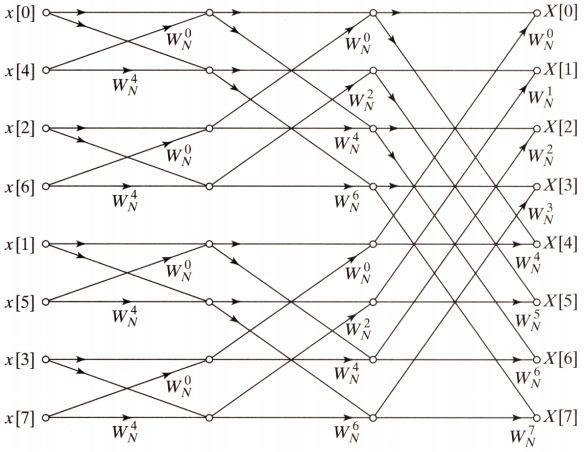
圖3是一個8點DIT FFT的完整架構圖。

圖3 DIT FFT

頻域抽取法

我們可以將DFT公式中的項目在頻域上重新分組，這樣就叫做頻域抽取（Decimation-in-frequency）。

首先先觀察在頻域上偶數項的部分：

再觀察在頻域上奇數項的部分：

上述的推導可以畫成下面的推導圖：

DIF-1

更進一步的拆解-point DFT的架構

DIF-2

圖4為8點FFT下-point DFT的架構

圖4 DIF-3

總結上述架構，完整的8點DIF FFT架構圖為

DIF-4

單一基底

利用庫利－圖基算法進行離散傅立葉拆解時，能夠依需求而以2, 4, 8…等2的冪次方為單位進行拆解，不同的拆解方法會產生不同層數快速傅立葉變換的架構，基底越大則層數越少，複數乘法器也越少，但是每級的蝴蝶形架構則會越複雜，因此常見的架構為2基底、4基底與8基底這三種設計。

2基底

2基底-快速傅立葉算法（Radix-2 FFT）是最廣為人知的一種庫利－圖基快速傅立葉算法分支。此方法不斷地將N點的FFT拆解成兩個'N/2'點的FFT，利用旋轉因子的對稱性藉此來降低DFT的計算複雜度，達到加速的功效。

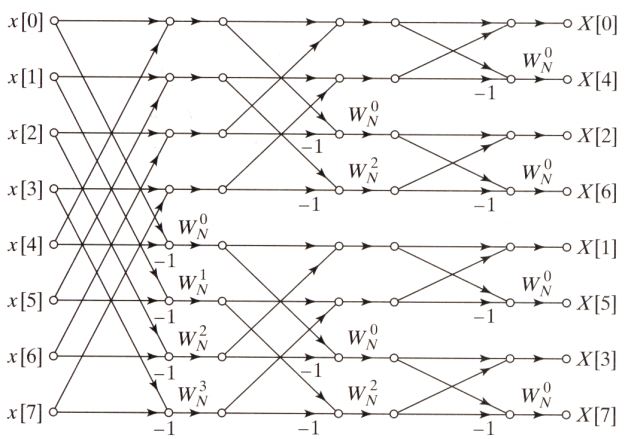
而其實前述有關時域抽取或是頻域抽取的方法介紹，即為2基底的快速傅立葉轉換法。以下展示其他種2基底快速傅立葉算法的連線方法，此種不規則的連線方法可以讓輸出與輸入都為循序排列，但是連線的複雜度卻大大的增加。

4基底

4基底快速傅立葉變換算法則是承接2基底的概念，在此里用時域抽取的技巧，將原本的DFT公式拆解為四個一組的形式：

在這裡再利用的特性來進行與2基數FFT類似的化減方法，以降低算法複雜度。

8基底

在庫利－圖基算法裡，使用的基底（radix）越大，複數的乘法與存儲器的訪問就越少，所帶來的好處不言而喻。但是隨之而來的就是實數的乘法與實數的加法也會增加，尤其計算單元的設計也就越複雜，對於可套用FFT之點數限制也就越嚴格。在表中我們可以看到在不同基底下所需的計算成本。

在DFT的公式中，我們重新定義x=[x(0),x(1),…,x(N-1)]T, X=[X(0),X(1),…,X(N-1)]T，則DFT可重寫為X=FN‧x。FN是一個N×N的DFT矩陣，其元素定義為[FN]ij=WNij(i,j ∈ [0,N-1])，當N=8時，我們可以得到以下的F8矩陣並且進一步將其拆解。

在拆解成三個矩陣相乘之後，我們可以將複數運算的數量從56個降至24個複數的加法。底下是8基底的的SFG。要注意的是所有的輸出與輸入都是複數的形式，而輸出與輸入的排序也並非規律排列，此種排列方式是為了要達到接線的最最佳化。

8基地-1

混合基底

2-8基底

在2/8基底的算法中，我們可以看到我們對於偶數項的輸出會使用2基底的分解法，對於奇數項的輸出採用8基底的分解法。這個做法充分利用了2基底與4基底擁有最少乘法數與加法數的特性。當使用了2基底的分解法後，偶數項的輸出如下所示。

奇數項的輸出則交由8基底分解來處理，如下四式所述。

以上式子就是2/8基底的FFT快速算法。在架構圖上可化為L型的蝴蝶運算架構，如圖5所示。

2-4-8基底

為了改進Radix 2/8在架構上的不規則性，我們在這裡做了一些修改，如下表.。此修改可讓架構更加規則，且所使用的加法器與乘法器數量更加減少，如下表所示。

N=8	2基底	4基底	2/4混合基底	2/4/8基底
8	2	-	2	0
64	98	76	72	48
512	1538	-	1082	824
4096	18434	13996	12774	10168

在這裡我們最小的運算單元稱為PE（Process Element）,PE內部包含了2/8基底、2/4基底、2基底的運算，簡化過的信號處理流程與蝴蝶型架構圖可見圖6

圖6 蝴蝶型架構圖

4基底

基底的選擇越大會造成蝴蝶形架構更加複雜，控制電路也會複雜化。因此Shousheng He和Mats Torkelson在1996提出了一個2^2基底的FFT算法，利用旋轉因子的特性：。而–j的乘法基本上只需要將被乘數的實部虛部對調，然後將虛部加上負號即可，這樣的負數乘法被定義為'簡單乘法'，因此可以用很簡單的硬體架構來實現。利用上面的特性，22基底FFT能用串接的方式將旋轉因子以4為單位對DFT公式進行拆解，將蝴蝶形架構層數降到log4N，大幅減少複數乘法器的用量，而同時卻維持了2基底蝴蝶形架構的簡單性，在性能上獲得改進。2^2基底DIF FFT算法的拆解方法如下列公式所述：

N點DFT公式：

利用線性映射將n與k映射到三個維度上面

然後套用Common Factor Algorithm（CFA）

而蝴蝶型架構會變成以下形式

利用旋轉因子的特性，可以觀察出

再將此公式帶入原式中可以得到

如上述公式所示，原本的DFT公式會被拆解成多個，而 又可分為BF2I與BF2II兩個層次結構，分別會對應到之後所介紹的兩種硬體架構。

一個16點的DFT公式經過一次上面所述之拆解之後可得下面的FFT架構

16點FFT架構

可以看出圖6的架構保留了2基底的簡單架構，然而複數乘法卻降到每兩級才出現一次，也就是 次。而BF2I以及BF2II所對應的硬體架構如圖7：

其中BF2II硬體單元中左下角的交叉電路就是用來處理-j的乘法。

一個256點的FFT架構可以由下面的硬體來實現：

圖8 22-128

其中圖8下方的為一7比特寬的計數器，而此架構的控制電路相當單純，只要將計數器的各個比特分別接上BF2I與BF2II單元即可。

下表將2基底、4基底與22基底算法做一比較，可以發現22基底算法所需要的乘法氣數量為2基底的一半，加法棄用量是4基底的一半，並維持一樣的存儲器用量和控制電路的簡單性。

8基底

如上所述，22算法是將旋轉因子視為一個簡單乘法，進而由公式以及硬體上的化簡獲得硬體需求上的改進。而藉由相同的概念，Shousheng He和Mats Torkelson進一步將旋轉因子 的乘法化簡成一個簡單乘法，而化簡的方法將會在下面講解。

在2基數FFT算法中的基本概念是利用旋轉因子的對稱性，4基數算法則是利用 的特性。但是我們會發在這些旋轉因子的對稱特性中出現。

─並沒有被利用到。主要是因為 的乘法運算會讓整個FFT變得複雜，但是如果藉由近似的方法，我們便可以將此一運算化簡為12個加法。

我們可以從上式注意到，可以被近似為五個加法的結果，所以 就可以被簡化為只有六個加法，再算入實部與虛部的計算，總共只需12個加法器就可以運用到此一簡化特性。

12adder_multi

經由與基底類似的推導，並用串接的方式將旋轉因子以8為單位對DFT公式進行拆解，基底FFT算法進一步將複數乘法器的用量縮減到log₈N，並同時維持硬體架構的簡單性。推導的方法與基底相當類似。藉由這樣的方法，基底能將乘法器的用量縮減到2基底的1/3，並同時維持一樣的存儲器用量以及控制電路的簡單性。