在計算機科學中，分治法是建基於多項分支遞歸的一種很重要的算法範式。字面上的解釋是“分而治之”，就是把一個複雜的問題分成兩個或更多的相同或相似的子問題，直到最後子問題可以簡單的直接求解，原問題的解即子問題的解的合併。
這個技巧是很多高效算法的基礎，如排序算法（快速排序、歸併排序）、傅立葉變換（快速傅立葉變換）。
另一方面，理解及設計分治法算法的能力需要一定時間去掌握。正如以歸納法去證明一個理論，為了使遞歸能夠推行，很多時候需要用一個較為概括或複雜的問題去取代原有問題。而且並沒有一個系統性的方法去適當地概括問題。
分治法這個名稱有時亦會用於將問題簡化為只有一個細問題的算法，例如用於在已排序的列中尋找其中一項的折半搜尋算法（或是在數值分析中類似的勘根算法）。這些算法比一般的分治算法更能有效地執行。其中，假如算法使用尾部遞歸的話，便能轉換成簡單的循環。但在這廣義之下，所有使用遞歸或循環的算法均被視作“分治算法”。因此，有些作者考慮“分治法”這個名稱應只用於每個有最少兩個子問題的算法。而只有一個子問題的曾被建議使用減治法這個名稱。
基本介紹
- 中文名：分而治之算法
- 外文名：Divide and rule method
- 使用者：君主和殖民者們
- 屬性：數學方法
- 數學方法：分解
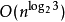
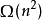
早期歷史上的先例,優勢,解決困難問題,算法效率,實現,循環遞歸,顯堆疊,示例,算法思想,
早期歷史上的先例
折半搜尋算法——一個將原來問題連逐地拆細成大約一半大小的單一子問題的分治算法——擁有一段悠長歷史。雖然算法在計算機上的清楚描述出1946年約翰莫齊利（John Mauchly）的一篇文章里，然而利用已排序的物件序列去加快搜尋的構想早已在公元前200年的巴比倫尼亞出現。另一個單一子問題的分治算法是找出2個數的最大公因數的輾轉相除法（透過將數位化小至使子問題變得簡單），於公元前數世紀已經出現。
一個早期有多個子問題的分治算法是高斯在1805年描述關於快速傅立葉奱換的算法，儘管他沒有量化地分析它的運算元目，而快速傅立葉奱換直至在一世紀之後被重新發現之前亦沒有廣泛流傳。這個算法現稱為庫利－圖基快速傅立葉變換算法。
至於專門用於計算機之上而且正確地分析的分治算法早期例子，則可以數到約翰·馮·諾伊曼於1945年發明的歸併排序。
另一個顯著的例子是Anatolii Alexeevitch Karatsuba於1960年發明在
步驟內將兩個n位數相乘的Karatsuba算法。它反證了安德雷·柯爾莫哥洛夫於1956年認為這個乘法需要
步驟的猜想。
高德納舉了一個最初並沒有涉及計算機的分治算法例子，就是一般郵局用於分發信件的方法：信件在主要郵局根據不同的地理範圍而分到不同的袋裡，每個袋亦在運送到地區郵局時分到更小的袋裡，如是者直至信件被派發為止。這個方法與早於1929年的打孔卡排序機所用的基數排序相類同。
優勢
解決困難問題
分治算法是一個解決複雜問題的好工具，它可以把問題分解成若干個子問題，把子問題逐個解決，再組合到一起形成大問題的答案。比如，漢諾塔問題如果採用分治算法，可以把高度為n的塔的問題轉換成高度為n-1的塔來解決，如此重複，直至問題化簡到可以很容易的處理為止。
算法效率
實現
循環遞歸
在每一層遞歸上都有三個步驟：
- 分解：將原問題分解為若干個規模較小，相對獨立，與原問題形式相同的子問題。
- 解決：若子問題規模較小且易於解決時，則直接解。否則，遞歸地解決各子問題。
- 合併：將各子問題的解合併為原問題的解。
顯堆疊
示例
以下是歸併排序C語言的示例代碼，輸入參數中，需要排序的數組為array[],起始索引為first，終止索引為last。調用完成後，array[]中從first到last處於升序排列。
void merge_sort(int array[], unsigned int first, unsigned int last) { int mid = 0; if(first<last) { mid = (first+last)/2; merge_sort(array, first, mid); merge_sort(array, mid+1,last); merge(array,first,mid,last); } }在程式中可以看出分治法的套用：在merge_sort()中，將原來針對索引first到last的數組排序的問題，分為二份較小的問題
- 先針對索引first到mid的數組排序。
- 再針對索引mid+1到last的數組排序。
最後再進行二個數組的合併。
算法思想
分而治之方法與軟體設計的模組化方法非常相似。為了解決一個大的問題，可以：
1) 把它分成兩個或多個更小的問題；
2) 分別解決每個小問題；
3) 把各小問題的解答組合起來，即可得到原問題的解答。小問題通常與原問題相似，可以遞歸地使用分而治之策略來解決。
