公式
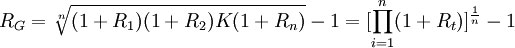
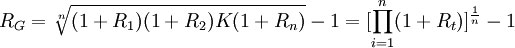
幾何平均收益率是將各個單個期間的收益率乘積,然後開n次方。幾何平均收益率使用了複利的思想,即考慮了資金的時間價值,也就是說,期初投資1元,第一期末則值(1 +...
定義 幾何平均報酬率是採用時間加權平均法(Time Weighted Average)來計算的報酬率。這種方法是把所有現金股利再投資於以後各期作為假設,因此,這種方法是測定期初價值...
年化收益率僅是把當前收益率(日收益率、周收益率、月收益率)換算成年收益率來...這種情況下,便有兩種方法來計算年化收益率,第一種是幾何平均的方法,即先計算...
就是現代投資組合理論的基石,馬科維茨將其定義為風險投資的戰略性資產平均增長...//幾何收益率g的6種均值方差逼近//不同類別資產的觀測近似誤差...
股權風險溢價ERP(equity risk premium)是指市場投資組合或具有市場平均風險的股票收益率與無風險收益率的差額。從這個定義可看出:一是市場平均股票收益率是投資者在...
一、幾何平均收益率方法二、安全第一方法附錄3-1 效用函式與均值一方差分析附錄3-2 對數效用函式與最高幾何平均收益率附錄3-3 無風險借貸條件下的安全第一標準...
票的收益率。在其他情況下,尤其是在需要解釋資產價值的實際增減情況時,通常使用幾何平均收益率。(3)時間權重收益率以時間為權重的收益率簡稱時間權重收益率。之所以...
1.3.2 總收益率10 1.3.3 時間加權收益率10 1.3.4 資金加權收益率12 1...13.5.1 使用算數平均超額收益265 13.5.2 使用幾何平均超額收益265 13.5.3...
附錄1B算術平均回報率和幾何平均回報率/19第2章風險、收益和資產配置:為什麼長期股票風險小於債券/20風險和收益的衡量/20風險和持有期限/21市場高點時的投資者收益...
3.10 計算權益收益率3.11 本章小結習題附錄1:計算負數利潤時的自由現金流...附錄2:連續復收益與幾何平均收益9 計算沒有賣空限制的有效投資組合...
它討論的是投資市場適者生存問題,或者說如何提高長期投資的幾何增長平均速度問題,...2.1.1 收益率和產出比 15 2.1.2 收益的機率預測 16 2.1.3 期望收益和...
