幻影思維學

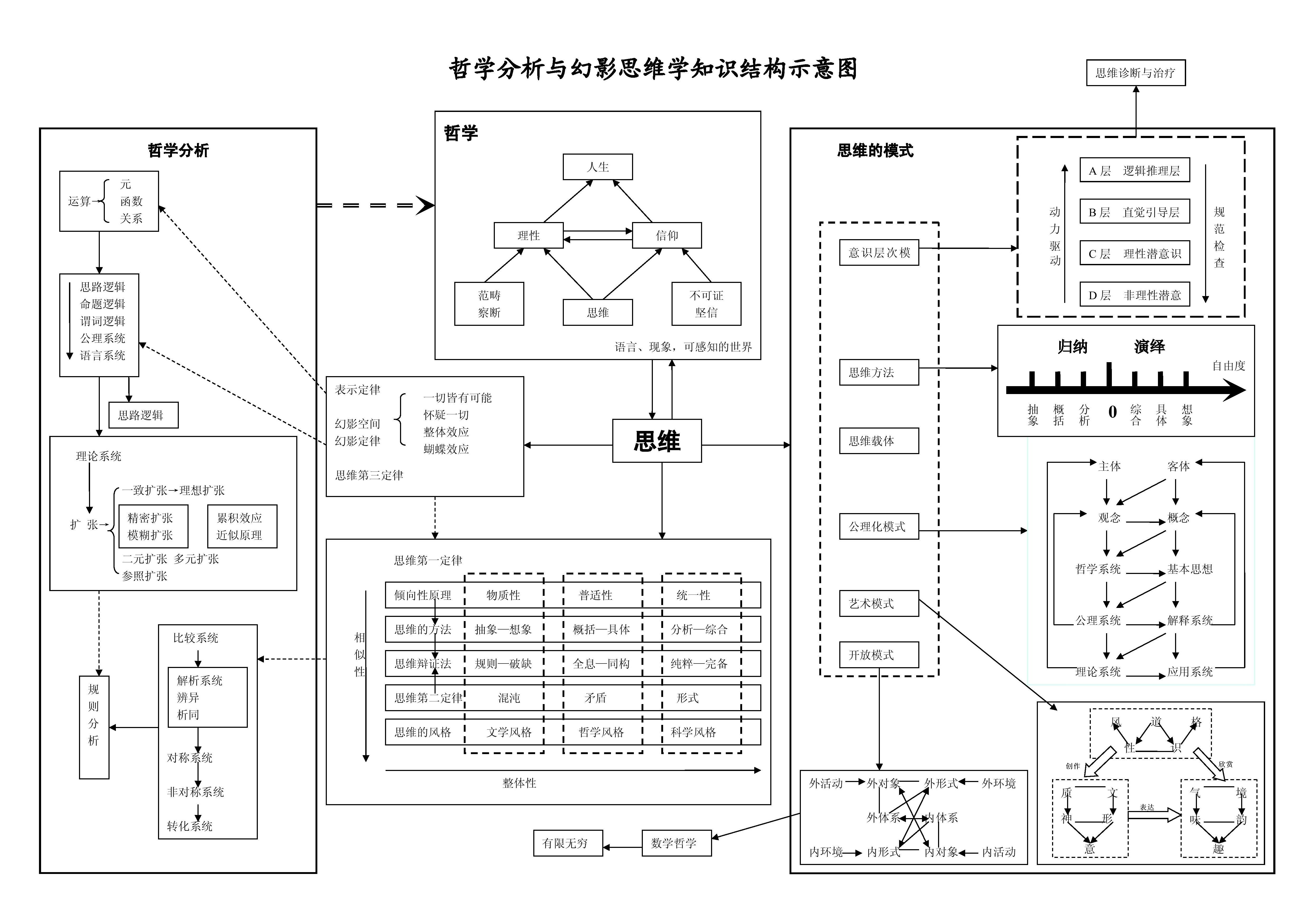
幻影思維理論（幻影思維學）是對思維進行反思的結果，理論主要包含比較系統、思維的傾向性、運算、邏輯系統、理論系統、幻影空間等六個部分。

基本介紹

• 中文名：幻影思維學
• 外文名：phantom thinking
• 學科歸屬：思維科學，思維學
• 理論創始人：高海

幻影思維理論

幻影思維理論是對自己的思維進行反思的結果，幻影思維理論是從思維的內容的角度對思維進行的研究，思維的內容包含但並不限於知識、科學理論體系，任何觀念、觀點及其形成的體系，哪怕是虛構的錯誤的，也包含在內。理論主要包含比較系統、思維的傾向性、運算、邏輯系統、理論系統、幻影空間等六個部分。

比較系統部分認為對認知對象進行比較是思維的基本功能，用公理化的方法構建了一個形式化公理系統。思維的傾向性認為思維過程的發展具備一種傾向性，不是毫無目的毫無規律的。運算用公理化的方法定義了元、運算、函式、命題等並作為表示思維的工具。邏輯系統是對邏輯進行思考，形成的對邏輯、數學和語言的認識。理論系統是在指元及相關的函式命題按照一定規則組合形成的系統。幻影空間是以理論系統為基礎構建的描述思維觀點真假性質的一個理想模型。幻影思維理論這個名稱便取自幻影空間。

1、比較系統

1.1 比較系統

比較系統是由元{T,Y}，函式J，和下列命題構成的理論系統：

命題1：

（1） J(T,T)=T

（2） J(T,Y)=Y

（3） J(Y,Y)=T

（4） J(Y,T)=Y

可解釋為：

(1) 同與同相同

(2) 同與異相異

(3) 異與異相同

(4) 異與同相異

異即不同，同即無異。

1.2 比較系統的擴張

命題1刻畫了一個有限元的比較系統，然而所要比較的事物卻包羅萬象，不僅僅是異與同兩者。因此有必要擴充比較事物的範圍，即比較系統第一次擴張。擴充比較事物的範圍須引入以下命題：

命題2：任何事物與自身的比較關係為同，否則為異。

一般來說，一事物與一事物的相同，和另一事物與另一事物的相同，雖然比較結果都是同，但是同與同之間還是有所差別的。同樣，異與異也是不完全相同的。因此，比較系統第一次擴張後，還要進行第二次擴張即擴充比較結果，使其更精確。擴張後的比較系統，運算元與結果元均為x₁,x₂,x₃,…，運算元與運算J構成新的比較系統：

J(x_i,x_j)= x_k。

1.3 解析系統

在J(x_i,x_j)=x_k中，將x_k解析為結構(m,t_i,t_j)即x_k=(m,t_i,t_j)。並且定義新運算F_h,X_t,B_y,使得任意x_i,x_j ，若 J(x_i,x_j)=x_k=(m,t_i,t_j)則

F_h(m,t_i)=x_i 複合運算

F_h(m,t_j)=x_j 複合運算

X_t(x_i,x_j)= X_t(x_j ,x_i)=m 析同運算

B_y(x_i,x_j)=t_i ，B_y(x_j,x_i)=t_j 辨異運算

由J，F_h,X_t,B_y,等運算及相應的元組成的比較系統稱為解析系統。

1.4思維第一定律

思維第一定律：思維的基本方式是解析比較，基本方法是辨異和析同。

1.5 對稱系統

在解析系統中，關注的是比較、複合、析同、辨異等運算，若關注的是x_i，x_j，m，t_i，t_j 等運算元，則稱該系統為對稱系統，x_i，x_j，m，t_i，t_j等元稱為規則。其中x_i，x_j稱為混沌，m稱為矛盾，t_i，t_j稱為條件。特別的，運算複合F_h稱為形式。

1.6 規則分析

在一定的理論系統中，將x_i解析為矛盾m，條件t_i，並得出x_i =F_h(m,t_i)的過程，稱為規則分析。分析所得的規則的總體，稱為被分析規則的相對規則度。在一定理論系統中，不可進一步解析的規則稱為該理論系統的基本規則，將規則分析為基本規則，所得規則的全體，稱為該規則得絕對規則度。將規則進行分析，所得可被進一步分析而不進行進一步分析的規則的規則度之總和，稱為該規則的模糊度。

1.7 非對稱系統

對於兩個規則x_i：x_j，如果關注於通過x_j而了解x_i，令x_k=(x_i：x_j)，則稱x_k為修辭，稱x_i,x_j為語言描述，X_t(x_i,x_j)稱為x_j對x_i的修辭有效，B_y(x_i,x_j) 稱為x_j對x_i的修辭模糊，B_y(x_j, x_i) 稱為x_j對x_i的修辭錯誤。

將x_k作為混沌規則進行規則分析，即x_k= F_h(m,t)，則稱形式F_h為修辭x_k的邏輯。語言描述與其修辭的邏輯構成的系統稱為語言系統，語言描述及其修辭統稱文學作品。文學作品及其間關係的總和，稱為文學系統，簡稱文學。

1.8 轉化系統

若關注於修辭A與其相應的邏輯L的內在關係，將其作為新的規則S，令S=(L|A)，對S進行分析，得出S= F_h(m,t)。則稱S為數學套用，稱F_h為數學理論。

若關注於S的正確性(合理性)，並且認為S是正確的(合理的)，則稱S為科學，稱m為(相應的)哲學。

2、思維的傾向性

2.1 傾向性原理

傾向性原理：人類思維起源和來源於物質世界，思維的內容穩定在同一理論系統中，但具有向普遍適用和高度統一發展的傾向。

傾向性原理是說明思維具有物質性、穩定性、普適性和統一性。

物質性表明人類思維即意識運動是物質運動的高級形式，並且思維的內容是對物質世界的反映。思維起源和來源於物質世界，不能脫離客觀現實無中生有。

穩定性是指思維的內容結果在一定的時間內是相對穩定的，只有通過學習頓悟或者遺忘等過程才會發生質的變化。

普適性是指人類思維傾向於將此處得到的結論擴大化套用於彼處。這種擴大化套用可能是正確的，也可能是不正確或不完全正確的，但這種傾向是客觀存在的。這是人類思維發揮主觀能動性的前提。

統一性是指人類思維傾向於用同一理論去解釋不同的現象。從而使解釋不同現象的不同理論統一為同一種理論。雖然在一定的歷史條件限制下，這種統一未必能得以實現，但這種傾向仍然是存在的。這種統一性體現了人類思維和相應科學理論的發展水平。

普適性與統一性是從不同的角度說明同一問題的兩個方面。從哲學的角度講，是客觀世界的形態多樣性與物質統一性決定了人類思維內容的普適性與統一性。在後面可以看出，是思維自身為這種普適性與統一性提供了可能性。只有兩方面結合起來，這種可能性才得以實現。

2.2 思維方法

與思維的傾向性相對應的思維的方法主要包括：抽象、想像，概括、具體，分析、綜合、歸納、演繹等，從思維的自由度的角度考察這些方法，可以分為4組，如圖所示：

Ⅰ)抽象——想像

人類思維的內容來源於物質世界，但並不等價於物質世界，這是抽象思維在起作用。人類思維要具有創造性，要反作用於物質世界，則是想像思維在起作用。其實抽象中不乏想像，想像中不乏抽象，二者無法截然分開，只是分析問題的角度以及分析問題的主導矛盾不同而已。

Ⅱ)概括——具體

人類思維具有普遍適用的傾向，而不僅僅適用於個別現象，普適性要求概括，只有高度概括，才能普遍適用。但思維要套用於一個特定的問題，解釋一特殊現象，這就需要具體思維。於是產生了概括——具體這一組思維方法。

Ⅲ)分析——綜合

客觀世界往往是錯綜複雜的，並非簡單的因果關係，而人類思維具有統一的傾向。要理清事實真相併且以統一的理論解釋各種錯綜複雜的現象，就需要分析——綜合這一人類思維中最成熟也最為有力的武器。客觀世界是聯繫的、發展的，只有套用分析與綜合的方法才能理清其中聯繫，認識事物的發展規律。

這三組方法都是思維基本方法即辨異——析同在不同場合下不同組合的具體反映。三者之間是水乳交融無法截然分開的。這是因為三者之間的差別同抽象與想像之間的差別一樣，是由於看問題的角度與分析問題的主導矛盾不用造成的。

另外還有一組思維方法：歸納——演繹，該方法與概括——具體非常相似。它只是人類思維保持嚴謹的一種邏輯手段，表明了兩種不同的思維方向，而不是和上述三組方法等並列的思維方法。

2.3 思維第二定律

抽象、想像，概括、具體，分析、綜合三組方法的自由度是不同的，抽象、想像的自由度最大，思維具有很大的不確定性，這時的思維形態用混沌表示。概括、具體的自由度和不確定性居中，這時的思維形態用矛盾表示。分析、綜合的自由度和不確定性最小，這時的思維形態用形式表示。因此按照自由度的大小，就可以將思維形態分為三種，即

思維第二定律：思維的基本形態是混沌、矛盾和形式。

2.4 思維辯證法

據思維第二定律思維形態包括混沌、矛盾和形式，混沌的基本性質是規則、破缺，矛盾的基本性質是全息、同構，形式的基本性質是純粹、完備。

所謂規則，是指事物運動的必然性，任何事物，無論多么複雜，總有其運動規律。所謂破缺，是指事物運動的偶然性，任何事物，無論多么有規律，總不能被該規律所完全描述。這一對矛盾描述了混沌的基本性質。

所謂全息，是指事物的一部分總蘊涵了該事物的全體信息。所謂同構，指事物的結構及其各部分的結構總是相同或相近的。這一對矛盾描述了矛盾的基本性質。

所謂純粹，是指事物屬性的單一性表明某類事物的任意個體都具有該類事物所共有的屬性。所謂完備，是指事物或其屬性不多不少、不添不漏的完全與完整性。這一對矛盾描述了形式的基本性質。

規則、破缺，全息、同構，純粹、完備這三對矛盾便構成了思維辯證法的主要內容。

2.5 思維風格

考查文學、哲學與科學的思維風格，文學風格其思維的自由度是最大的，甚至風馬牛不相及的事物也可以聯繫在一起。科學風格則與此相反，科學思維的自由度是最小的，它以客觀嚴謹而著稱。哲學風格處於兩者之間，既不象文學那樣自由散漫，又不象科學那樣不敢越雷池一步。其主要作用在於指導人類的思維。這樣，思維方法就可以按自由度劃分為三種基本類別，即文學風格，哲學風格和科學風格。

文學風格，哲學風格和科學風格分別與混沌、矛盾、形式三種思維形態相對應，分別與抽象——想像、概括——具體、分析——綜合三種思維方法相對應，分別與規則——破缺、全息——同構、純粹——完備這三組矛盾相對應，分別與思維內容的來源、普遍適用的傾向、高度統一的傾向相對應。

3、運算

3.1　運算　代換

如果A形如R(a) ∣→ b ,則稱A為一個運算。a,b為元，a為運算元，b為結果元，R為運算法則，∣→ 為運算標誌符號。一般來說，不同的運算，R,a,b, ∣→ 是不同的，但卻具有相同的形式，即形式R(a) ∣→ b 的各部分是可能被其它元或法則或符號所代換的，代換後保持形式不變。若(a)為(a₁,a₂)所代換，則稱R(a₁,a₂) ∣→ b 為二元運算，同樣，稱R(a₁,a₂,a₃) ∣→ b為三元運算，R(a₁,a₂, a₃,…,a_n)∣→ b稱為n元運算。

3.2 逆運算

對於n元運算R(a₁,a₂, a₃,…,a_n)∣→ b , a_i與b互換位置得運算R(a₁,a₂, a₃,…, b,…,a_n)∣→ a_i稱為R(a₁,a₂, a₃,…,a_n)∣→ b的第i元逆運算，當i為1時，R (b,a₂, a₃,…,a_n)∣→ a₁稱為第1元逆運算；當i為n時，R (a₁,a₂, a₃,…, b)∣→ a_n稱為第n元逆運算。對n元運算R(a₁,a₂, a₃,…,a_n)∣→ b進行有限次求逆，包含自身在內，共可衍生運算 (n+1)! 個，結果元分別為a₁,a₂, a₃,…,a_n，b的各n!個。

3.3　運算性質

對二元運算R(a₁,a₂)∣→ b，可記作a₁Ra₂∣→ b ，簡稱R。若a₁Ra₂∣→ b ，則a₂Ra₁∣→ b ，稱該運算是可交換的，即R滿足交換律。

若(a₁Ra₂)Ra₃∣→ b ，則a₁R(a₂Ra₃)∣→ b ,稱R是可結合的，即運算R滿足結合律。

若aRa∣→ a，則稱R為積冪的，即運算R滿足積冪律；若aRa∣→ a，則稱R為等冪的, 即運算R滿足等冪律。

兩個二元運算R₁ R₂，若a₁R₁(a₂R₂a₃) ∣→ b ，則(a₁R₁a₂)R₂(a₁R₁a₃)∣→ b ，稱R₁對R₂是左分配的；若(a₂R₂a₃) R₁ a₁∣→ b ，則(a₂R₁a₁)R₂(a₃R₁a₁)∣→ b ,稱R₁對R₂是右分配的。若R₁對R₂既是左分配的，又是右分配的，則稱R₁對R₂是分配的，即運算R₁ R₂滿足R₁對R₂的分配律。

3.4　函式　反函式

對於運算R(a) ∣→ b，若關注於a與b在R規則下的對應性，從而在研究a變化時R(a) ∣→ b的整體性質，則R(a) ∣→ b稱為函式，a稱為自變數，R(a)與b稱為因變數或函式。其本質上依然是運算。函式R(a) ∣→ b研究的是R(a) ∣→ b運算特性，而研究R(a) ∣→ b的逆運算R (b) ∣→ a中b與a的對應特性的函式R (b) ∣→ a稱為R(a) ∣→ b的反函式。

3.5　命題　關係

對於運算R(a) ∣→ b，若關注於a滿足R(a) ∣→ b，則稱R(a) ∣→ b為關於a的一個命題，可簡記以A(a)。其本質上依然是運算。對於二元運算R(a₁,a₂) ∣→ b ，關注於a₁,a₂滿足R(a₁,a₂) ∣→ b 時，稱R(a₁,a₂) ∣→ b 為關於a₁,a₂的一個二元關係，可簡記作A(a₁,a₂)或a₁Aa₂，因此，命題也可稱作關係。對於二元關係A(a₁,a₂)，若A(a₁,a₂)成立，則A(a₂,a₁)成立，則稱關係A為交換的。

若，a₁Aa₂, a₂Aa₃則a₁Aa₃,則A稱為傳遞的，若A(a₁,a₂)，則B(a₂,a₁)，且B(a₁,a₂)，則A(a₂,a₁)，則稱A,B互為對稱關係。

若二元關係A是可傳遞的，則其對稱關係B也是可傳遞的。

若運算R(a₁,a₂) ∣→ b 是可交換的，則對應的關係R(a₁,a₂) ∣→ b 是可交換的若關係A是可傳遞的，又是可交換的，則稱A為等價的，其對稱關係亦為A

3.6 表示定律

一切事物是發展的，變化的，聯繫的。反映于思維中，可以用元、函式、命題等表示。

表示定律：思維中的任何事物可以用元表示，而事物的任何發展、變化、聯繫等性質特徵可以用運算、函式、命題、關係來表示。

4、邏輯系統

4.1思路邏輯

最簡單的邏輯，其中的命題只考慮真命題，沒有假命題，不考慮否命題，也不考慮與和或兩種命題關係。是用來表示思路的，故稱思路邏輯。思路邏輯，是最簡單最原始的邏輯形式。

思路邏輯的核心是推理規則，即已知A，(A->B)，則B，公式是(A,(A->B))->B

->是蘊含，推導的意思，表示前面的條件可以推導出後面的結果。

4.2邏輯系統的擴張

思路邏輯是最簡單最原始的邏輯形式，是可以擴張的。邏輯有兩個要素，命題，命題連線詞。邏輯系統的擴張，也有兩個方面，即連線詞擴張和命題結構擴張。

連線詞擴張就是根據需要，增添新的連線詞，如命題邏輯中增加了與、或、非等連線詞，而且命題有了真假之分。命題結構擴張，就是命題不再是簡單的命題，如謂詞邏輯中增加了命題變項，和謂詞的概念，一個命題是由謂詞和若干命題變項構成的。實際上，謂詞邏輯並不是簡單的命題結構擴張，而是思路邏輯先經過連線詞擴張為命題邏輯，再通過命題結構擴張為謂詞邏輯。

4.3命題邏輯

思路邏輯經過連線詞擴張，命題增加真假屬性，再增加新的連線詞，如與、或、非，就可以擴張為命題邏輯。命題真值除了真假之外，還可以由另外一種屬性，已知、未知，命題真值已知的就是命題為真或者假，未知的就是命題真假不確定，這樣的話，又可以擴張為三值邏輯。當然，如果增加新的範疇新的解釋，也可以擴張為n值邏輯，或者增加其它新連線詞，擴張為其它的邏輯系統。

4.4謂詞邏輯

在命題邏輯的基礎上，將命題解析成謂詞和命題變項的的形式，再增加新的連線詞，如存在，任意等，就形成了謂詞邏輯，謂詞邏輯是連線詞和命題結構兩方面的綜合擴張。

命題的結構，除了可以解析為謂詞與命題變項之外，還可以解析為其它的結構形式，比如自然語言語法的結構形式，這樣的話，就可以形成一種新的邏輯系統，當然，這種新的邏輯系統或許只是謂詞邏輯的一種等效形式。

4.5公理化系統

邏輯系統只對命題及其連線詞進行研究，如果對部分命題用公理進行約束，形成新的系統，就成為形式化公理系統。數學就是形式化公理系統的例子，部分物理也可以用公理化系統進行描述，數學研究的就是形式，公理化沒什麼問題。使用更大程度上使用數學工具，是一門科學成熟的標誌，但是對於物理等具體科學而言，公理化體系是沒有靈魂的工具，經驗的哲學沉思才是靈魂。

4.6語言系統

如果邏輯系統的所有連線詞、謂詞、變項都賦予具體的、特定的現實意義，那么這個系統就可以用來描述現實世界，而不再是純粹的形式系統，這時，邏輯系統就變成了語言。

4.7邏輯規律

邏輯存在於具體理論系統中，系統滿足矛盾律、排中律、同一律等其實是人們對具體系統的一種期待，這些性質規律是約束具體理論系統的，而不屬於邏輯系統。

命題間的推理關係形成一種邏輯網路，這種邏輯網路中命題的真值狀態，一般是穩定的，但是如果該理論體系中存在悖論的話，那么理論體系中的真值狀態就像震動一樣，是在不同的真值之間震盪的。

如果要求理論體系符合矛盾律的話，羅素悖論中的集合，其實是像萬能的上帝一樣，是一個虛構的，實際上並不存在的集合。

5、理論系統

5.1　理論系統　幻影空間 擴張

理論系統X_i指一個元素集合(論域)Y_i：{x_i，x_i,…}，相應的函式集合H_i :{f_i,f_i ,…}和相應的關係集合G_i：{A_i ,A_i ,…}按一定規則組合的系統。

f是X_i到X_j的函式，即：

1) f(Y_i)={f(x_i),f(x_i),…}Í{x_j,x_j,…}=Y_j;

2) f(H_i)={f(f_i),f(f_i),…}Í{f_j,f_j,…}=H_j;

3) f(G_i)={f(A_i),f(A_i),…}Í{A_j,A_j,…}=G_j。

則稱f為X_i到X_j的擴張，亦可稱X_j為X_i的f擴張。

5.2 一致擴張

f是X_i到X_j的擴張，稱X_j為X_i關於f_i的一致擴張，如果：

(1)("x_i)(f(f_i (x_i))=f(f_i)(f(x_i)));

稱 X_i為X_i關於A_i的一致擴張，如果：

(2)("x_i)(A_i (x_i)®f(A_i)(f(x_i)));

稱X_j為X_i關於x_i的一致擴張，如果：

(3)("f_i)(f(f_i (x_i))=f(f_i)(f(x_i)));

(4)("A_i)(A_i (x_i)®f(A_i)(f(x_i)))。

關於x_i，f_i與A_i的一致擴張統稱一致擴張，稱一致擴張為絕對一致擴張，如果任意k=1， 2，…，(1)(2)式成立或任意l=1，2，…，(3)(4)式成立。

5.3 理想擴張

X_j是X_i的絕對一致擴張，稱X_j為X_i關於f_i的半理想擴張，如果：

(1)("x_i)($x_j) (x_j=f(f_i(x_i)));

(2)("x_i)($x_j) (f(x_i)=f(f_i)(x_j)))。

半理想擴張稱為全理想擴張，如果：

(3)("x_i)("x_i)(f(f_i)(f(x_i))=f(f_i)(f(x_i))®f(x_i)=f(x_i)))

稱 X_j為X_i的絕對理想擴張，如果對所有k=1,2… (1),(2),(3)式成立.

5.4 精密擴張與模糊擴張

X_j是X_i的f擴張，X_i是X_j 的g擴張稱 X_j是X_i關於x_i的精密擴張，如果：

($x_j)($ x_j) ( ( ～(x_j=x_j))Ù(x_i=g(x_j)=g(x_i)))

並且稱X_i為X_j關於x_j,x_j的模糊擴張，用同樣的方法可以定義關於f_i,A_i的精密擴張，模糊擴張。

稱X_j為X_i的絕對精密擴張，如果X_j為X_i關於所有元素x_i，所有函式f_i，和所有關係A_i的精密擴張。

稱X_i是X_i的混合擴張，如果：

(1)X_j為X_i關於某些元素x_i，或某些函式f_i，或某些關係A_i的精密擴張;

(2)X_i為X_j關於某些元素或某些函式或某些關係的精密擴張。

5.5 積累效應　近似原理

X_i是X_j的g模糊擴張，X_j是X_i的f精密擴張，稱x_i為g(x_j) 的近似值，如果:

(1)x_i=g(x_j)

(2)($x_j)(x_i= g(x_j))

(3)～(x_j=x_j)

因取近似值而產生矛盾命題(A_i(x_i)Ù～(A_i(x_i))，　本質上是f(A_i)(x_j)Ù～(A_i(x_j))而非真正的矛盾命題。這種現象稱為積累效應或累積效應。經無窮步驟產生的積累效應稱為無窮效應。

當積累效應不明顯或在一定範圍內不足以產生矛盾時， x_i作為g(x_j) ,g(x_j)近似值仍然式理論系統近似有效，這就是近似原理。

同樣可以定義函式與關係的近似值集相應的積累效應。

5.6 二元一致擴張

如果考慮二元函式與二元關係，可以定義二元一致擴張與二元理想擴張以及相應的多元擴張，稱X_j是X_i關於(x_i,x_i)的二元一致擴張，如果：

(1)f(f_i (x_i, x_i))=f(f_i)(f(x_i),f(x_i)))；

(2)A_i(x_i, x_i)®f(A_i)(f(x_i),f(x_i)))。

對所有k=1,2,…都成立。

用同樣的方法可以定義關於f_i的二元一致擴張，即對任意(x_i, x_i)(1)式成立，關於A_i的二元一致擴張，對任意(x_i, x_i)(2)式成立。

稱X_j是X_i的二元(或三元)絕對一致擴張，如果對所有k,l,m(1),(2)式成立。

二元理想擴張 X_j是X_i的一個二元絕對一致擴張。稱X_j是X_i關於f_i的二元理想擴張，如果：

(1)("x_i)("x_i)($x_j) (x_j=f(f_i(x_i,x_i)));

(2)("x_i)($x_j) ($x_j) (x_i=f(f_i(x_i,x_i)))

稱二元理想擴張為二元全理想擴張，如果:

(3)("x_i)("x_i)("x_i)("x_i)(f(f_i(x_i,x_i))=f(f_i(x_i,x_i))®(f(x_i),f(x_i))=(f(x_i), f(x_i))

X_j是X_i的二元絕對理想擴張，如果任意k=1,2,3,…使(1),(2),(3)是成立。同樣，可以定義三元理想擴張，三元絕對理想擴張等。

5.7 參照 同構

若X_j是X_i的關於x_i的f精密擴張， X_i是X_j關於x_j的g模糊擴張，即x_i=f(x_j), x_j =g(x_i)。

若關注與研究x_i而研究f(x_j)(側重於結構)，則稱g(x_j)為x_i的一個微觀結構。若關注於研究x_j而研究f(x_i)(側重於背景)，則稱x_i為x_j的宇觀背景。微觀結構、宇觀背景所屬的系統稱為參照系。

若X_j是X_i的絕對一致擴張，並且X_i是X_j的絕對一致擴張，則稱X_j與X_i是同構的。

6、幻影空間

6.1 幻影空間與幻影定律

幻影空間是描述思維觀點真假性質的一個理想模型。

幻影空間S是由一些理論系統X組成並滿足以下條件的組合：

任意命題A，存在理論系統X_i X，使得命題A成立，並且存在理論系統X_j，使得命題A不成立

約定符號表示如下：

("A)(( $X_i) X_i→A)∧(($X_j)X_j→～A)

即一切皆有可能。

幻影定律：思維的全部內容，屬於同一幻影空間。

6.2 其他表現形式

除了一切皆有可能之外，命題的相對性還有其他的表現形式，如“懷疑一切”、“蝴蝶效應”、“細節決定成敗”、“整體大於部分之和”等，都可以用命題真假的相對性加以解釋。

懷疑一切：懷疑一切是與一切皆有可能等價的，在形式邏輯中，用P表示一個命題，則P的否命題非P也是一個命題，既然任何一個命題，都會有一種條件存在，在這個條件下該命題為真命題。那么對於非P這個命題，也會有一種條件存在，使得非P是真命題。如果非P是真命題，那么P就是假命題，也就是說，任何命題P，都不是絕對正確的，是值得懷疑的。如果承認一切皆有可能，那么懷疑一切也是合理的，兩者是等價的。即懷疑一切是命題真假相對性的一種表現形式。

整體效應： 任意命題A、B，存在系統X_i和命題C，使得A導出C不成立， B導出C不成立但是A並且B導出C成立，即

("A)("B)($X_i)($C)X_i→((～(A→C)∧～(B→C))∧(A∧B)→C))

蝴蝶效應： 任意命題A、B存在理論系統X_i使得A導出B，即

("A)("B)($X_i)X_i→(A→B)

蝴蝶效應，通俗的說法是：“一個蝴蝶在巴西輕拍翅膀，可以導致一個月後德克薩斯州的一場龍捲風。”遠在巴西的蝴蝶輕拍翅膀（命題P），德克薩斯州的一場龍捲風（命題Q），蝴蝶效應就是P導致Q，看起來毫無關係的兩件事PQ，在特定的系統中，P導致Q是真命題，卻具有必然聯繫。馬蹄鐵效應、細節決定成敗、千里之堤毀於蟻穴、差之毫厘謬以千里等也是這個思想。

在形式邏輯中，P是命題，Q是命題，那么P導出Q也是命題，既然任何一個命題，都會有一種條件存在，在這個條件下該命題為真命題。對於命題P導出Q，也存在一個條件，在該條件下，命題P導出Q是真命題。也就是說，看是風馬牛不相及的兩個命題之間，在一定的條件下，也具備了因果關係。這就對是蝴蝶效應的解釋。

在形式邏輯中，P、Q、V是命題，其中P不能獨立導出V，Q不能獨立導出V，P與Q導出V也是命題，既然任何一個命題，都會有一種條件存在，在這個條件下該命題為真命題。對於命題P與Q導出V，也存在一個條件，在該條件下，命題P與Q導出V是真命題。也就是說，P、Q整合在一起，會導出一個新的命題V，這就是整體大於部分之和的解釋，從命題形式上講，整體大於部分和，也算是蝴蝶效應的一種。

6.3 思維第三定律

邏輯存在於具體的理論體系中，不是獨立存在的，但這個理論體系可以是邏輯本身。在推理規則 (A,(A->B))->B中，有兩個->，內層的->是由具體的理論體系所決定的，不是邏輯學的研究對象，外層的->是由邏輯規則所決定的，那么外層的->的推導結果是否可靠呢？答案是肯定的。如果前提條件是可靠地充分的，則其結果是可靠地。結果的可靠程度與理由的充分程度是一致的。即思維第三定律。

思維第三定律：思維的基本規則是理由相對充分，而且結果的可靠程度與理由的充分程度是一致的。

對於信或不信，可靠性取決於理由是否充足，是理性與信仰的綜合作用的結果。

6.4 思維與哲學

哲學的作用在於指導人們的思維，是研究萬物的最高學問，因此，哲學層次應“高於”萬物。思維，屬於是萬物的一分子，但是，思維不同於普通的事物，它是萬物之靈，萬物與思維，從包含範圍上講，萬物，包括思維，另外一方面，一切學問，都是思維的結晶，哲學也不例外，同樣是思維的產物，從這個角度講，思維又是先於哲學的。因此，哲學、萬物、思維，就形成一個循環：哲學>>萬物>>思維>>哲學>>……

作為思考者，所自由操控的就是思維，從思維開始，思索哲學。

思考者考慮問題時，思維是存在的。思維有具體的內容，可以來源於記憶、感覺、知覺、直覺、幻想、內省或者其它信息來源。感覺、知覺的內容是思考者所能察知的現象。現象的感知是真實的，錯覺、假象也是一種真實的感知。

思維的內容可以通過語言交流，但是語言是模糊的，不精確的，對語言的理解是相對的。有些事只可會意，不可言傳，會意也是模糊的。有時因為現象本身就是模糊的，只有模糊才是精確的，精確的反而是模糊的近似。語言需要辨析，但是更需要返璞歸真，需要回歸生活，按照直覺去理解語言最普通的模糊的現實意義。

理性是在經驗的基礎上分析現象認識世界形成知識，理性是形成知識的內驅力，經驗是形成知識的外推力，理性和經驗起始於人之初對世界的本能的感知。

思考者在範疇的框架內分析現象認識世界，範疇框架之外的則迷茫無知甚至視而不見，形式邏輯、辯證邏輯、甚至太極、兩儀、四象、八卦、三才、五行等都屬於認知範疇，而且範疇框架是發展變化的。對現象的感知是真實的，範疇的框架也是合理的，然而將合適的範疇套用於分析具體的現象，卻需要明察實斷，需要敏銳的直覺力、深邃的洞察力，正確的理論套用於不當的情景只會得出荒謬的結論。範疇如同公理化體系，是強大有力卻沒有靈魂的工具，對經驗的哲學沉思才是思維的靈魂。

思考者可以從以往的經驗、察知的現象出發獲取許許多多的知識，但是總有些東西是不可證的，或者說是現階段，在一定的歷史條件限制下是無法證實也無法證偽的，比如本源的問題、知識基礎的問題，還有“人心”的問題，對於這類問題，只能通過信仰去解決，堅定地信念去無條件的否定或無條件的相信。無論是否定還是確定，都會有爭議，沒有爭議，就沒有哲學。沒有理性的信仰是狂熱的，是失控的，沒有信仰的理性是漂泊的，是迷茫的。思維，就是在信仰的基礎上進行理性分析。

結束語

幻影思維理論是對思維的研究，但是其中對運算、比較、理論系統的公理化研究可以獨立出來自成體系，稱之為“哲學分析”，另外一部分就是將“哲學分析”作為工具對思維進行研究，即幻影思維（幻影思維學）。