平行線是指在同一平面內永不相交的兩條直線，判定平行線的方法包括1.同位角相等，兩直線平行2.內錯角相等，兩直線平行3.同旁內角互補，兩直線平行。
基本介紹
- 中文名：平行線的判定
- 外文名：Judgment of Parallel Lines
- 性質：判定
- 屬性：平行線
- 定義：永不相交的兩條直線叫做平行線
平行線的判定,平行線,特性,平行公理,判定方法,簡單的判定方法,結果,
平行線的判定
平行線
在同一平面內，永不相交的兩條直線叫平行線(parallel lines)。
特性
不平行兩條直線一定相交，平行用符號“∥”表示。在同一平面內，經過直線外一點，與直線平行的直線只有一條。
平行公理
“如果兩條直線被第三條直線所截，一側的同旁內角之和大於兩個直角，那么最初的兩條直線相交於這對同旁內角的另一側。”
這條公理的陳述過於冗長。在1795年，蘇格蘭數學家Playfair提出了以下公理作為平行公理的代替，在被人們廣泛的使用。
“在同一平面內，過直線外一點，有且只有一條直線與這條直線互相平行。”
平行公理的推論：（平行線的傳遞性）“ 如果兩條直線都和第三條直線平行，那么這兩條直線也互相平行。可以簡稱為：平行於同一條直線的兩條直線互相平行。”
判定方法
在同一平面內，兩條直線被第三條直線所截，如果同位角相等，那么這兩條直線平行。也可以簡單的說成：
1.同位角相等兩直線平行
在同一平面內，兩條直線被第三條直線所截，如果內錯角相等，那么這兩條直線平行。也可以簡單的說成：
2.內錯角相等兩直線平行
在同一平面內，兩條直線被第三條直線所截，如果同旁內角互補，那么這兩條直線平行。也可以簡單的說成：
3.同旁內角互補兩直線平行。
簡單的判定方法
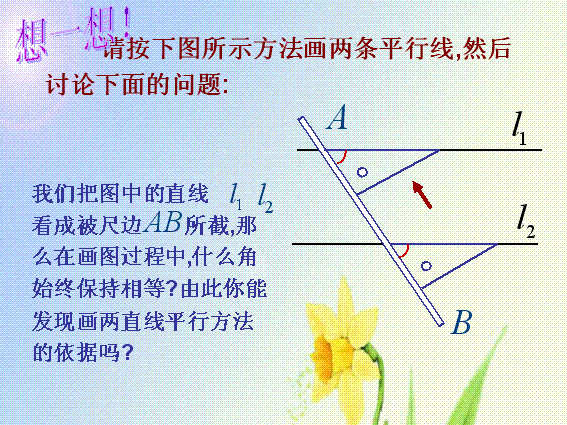
- 同位角相等，兩直線平行。
- 內錯角相等，兩直線平行。
- 同旁內角互補，兩直線平行。
- 在同一平面內，兩直線不相交，即平行、重合。
- 兩條直線平行於一條直線，則三條不重合的直線互相平行。
（相反判定方法） - 兩直線平行，同位角相等。
- 兩直線平行，內錯角相等。
結果
- 同一平面內，垂直於同一條直線的兩條線段（直線）平行
- （同一平面內），平行於同一條直線的兩條線段（直線）平行
- 同一平面內，永不相交的兩條直線叫平行線
- 過直線外一點有且僅有一條直線與已知直線平行
