兩條直線被第三條直線所截,在截線同旁,且在被截線之內的兩角,叫做同旁內角。同旁內角,“同旁”指在第三條直線的同側;“內”指在被截兩條直線之間。兩直線平行,同旁內角互補。同旁內角互補,兩直線平行。
基本介紹
- 中文名:同旁內角
- 外文名:Consecutive Interior Angles
- 定理:兩直線平行,同旁內角互補。
- 逆定理:同旁內角互補,兩直線平行。
- 判定:兩直線平行,同旁內角互補。
- 分類:數學
定義
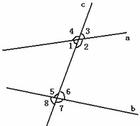 同旁內角
同旁內角特徵
定理以及逆定理
練習
區別
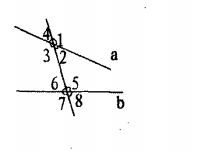
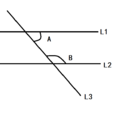
兩條直線被第三條直線所截,在截線同旁,且在被截線之內的兩角,叫做同旁內角。同旁內角,“同旁”指在第三條直線的同側;“內”指在被截兩條直線之間。兩直線平行,同旁內角互補。同旁內角互補,兩直線平行。
 同旁內角
同旁內角
兩條直線被第三條直線所截,在截線同旁,且在被截線之內的兩角,叫做同旁內角。同旁內角,“同旁”指在第三條直線的同側;“內”指在被截兩條直線之間。兩...
∠1與∠4,∠2與∠3在截線的同旁,且均在外方,稱為“同旁外角”。∠5與∠8,∠6與∠7在截線的同旁,且均在內方,稱為“同旁內角”。∠2與∠5,∠3與...
三線八角(three lines and eight angles)是幾種常見的位置相關角,指同一平面上的兩條直線被第三條直線所截形成的八個角,有同位角,內錯角,外錯角,同旁內角,同旁...
結識相交線中的新朋友同位角、內錯角、同旁內角[J]. 數學大世界:國中版, 2014(1):14-15. 2. 閆繼堂. 同位角、內錯角、同旁內角的辨別[J]. 國中數學教與...
兩條直線a,b被第三條直線c所截(或說a,b相交c),在截線c的同旁,被截兩直線a,b的同一側的角,我們把這樣的兩個角稱為同位角。兩條直線a,b被第三條直線c...
平行線是指在同一平面內永不相交的兩條直線,判定平行線的方法包括1.同位角相等,兩直線平行2.內錯角相等,兩直線平行3.同旁內角互補,兩直線平行。...
同旁內角:兩個角都在截線的同一側,且在兩條被截線之間,具有這樣位置關係的一對角互為同旁 內角。如:∠1和∠5,∠2和∠6。...
1 定義 2 領補角和對頂角 3 垂線 4 同位角、內錯角、同旁內角 相交線定義 編輯 兩條直線的位置關係:相交、平行。有唯一公共點的兩條直線叫作相交線。相交...
例如“兩直線平行,同旁內角互余”,這一命題的題設對應多種背景:對於其中所有背景,同旁內角都是互補而不是互余的。這個命題是一個假命題。...
3、同旁內角互補,兩直線平行。 如圖,CD∥EF [1] 4、兩條直線平行於第三條直線時,兩條直線平行。5、在同一平面內,垂直於同一直線的兩條直線互相平行。...
(2)兩條直線被第三條直線所截,如果同旁內角互補,那么這兩條直線平行。(同旁內角互補,兩直線平行)(3)兩直線都與第三條直線平行,那么這兩條直線也互相平行。(...
11 同旁內角互補,兩直線平行12兩直線平行,同位角相等13 兩直線平行,內錯角相等14 兩直線平行,同旁內角互補 [1] 計算公式三角形 15 定理 三角形任意兩邊的和大於...
根據同旁內角互補,兩直線平行可知,CD∥CD',這和CD與CD'交於C矛盾。∴假設不成立,即當C在直線外時,有且只有一條直線CD與AB垂直。...
互為餘角 互為補角 同旁內角 平行公理 性質定理 判定定理斜三角形 對應頂點 尺規作圖 基本作圖 互逆命題 互逆定理凸多邊形 平行線段逆否命題 對稱中心 等腰梯形...
兩條平行線被第三條直線所截,同旁內角互補(簡稱“兩直線平行,同旁內角互補”)。 兩條平行線被第三條直線所截,內錯角相等(簡稱“兩直線平行,內錯角相等”)。 ...
它說的是:如果一直線和兩直線相交,且所構成的兩個同旁內角之和小於兩直角,那么,把這兩直線延長,它們一定在那兩內角的一側相交。數學家們並不懷疑這個命題的真實...
12.較複雜的圖形中同位角、內錯角、同旁內角的位置關係的分析 13.直線相交時有關角的求法 5.2平行線及其判定 1.平行線的定義 2.平行公理及其推論 3....
3.兩直線平行,同旁內角互補互相平行判定方式 編輯 1.同位角相等,兩直線平行2.內錯角相等,兩直線平行3.同旁內角互補,兩直線平行互相平行推論 編輯 ...
11.同旁內角互補,兩直線平行12.兩直線平行,同位角相等13.兩直線平行,內錯角相等14.兩直線平行,同旁內角互補15.定理 三角形兩邊的和大於第三邊...
14 兩直線平行,同旁內角互補 15 定理 三角形兩邊的和大於第三邊 16 推論 三角形兩邊的差小於第三邊 17三角形內角和定理三角形三個內角的和等於180° 18 推論...
同旁內角互補; 兩直線平行。 符號:∥讀作“平行於” ‖在C語言編程 編輯 ‖定義 邏輯或[2] ,是邏輯運算符,符號是“||”(在PASCAL中為"or")。 “邏輯...
