矢量平行位移的概念是黎曼空間張量計算的重要的幾何學基礎。Levi-Civita最先聯繫到將黎曼空間Rn放置在歐幾里德空間Rn(n+1)/2內的辦法使矢量平行位移的概念列成公式,後來Wyel又作了進一步推導。
基本介紹
- 中文名:平行位移
- 外文名:parallel displacemen
- 所屬學科:數學
- 相關人物:列維-齊維塔、布勞威爾等
- 相關概念:黎曼空間、歐幾里得空間等
發展背景

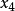
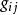
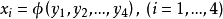
概念的提出
定義



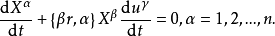
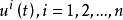
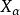

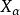

矢量平行位移的概念是黎曼空間張量計算的重要的幾何學基礎。Levi-Civita最先聯繫到將黎曼空間Rn放置在歐幾里德空間Rn(n+1)/2內的辦法使矢量平行位移的概念列成公式,後來Wyel又作了進一步推導。

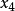
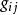
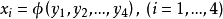



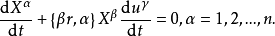
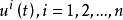
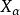

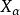
矢量平行位移的概念是黎曼空間張量計算的重要的幾何學基礎。Levi-Civita最先聯繫到將黎曼空間Rn放置在歐幾里德空間Rn(n+1)/2內的辦法使矢量平行位移的概念列成...
平行移動法是指一批零件中的每個零件在前一道工序完工後,立即傳送到下一道工序繼續加工的移動方式。...
位移(displacement)用位移表示物體(質點)的位置變化。定義為:由初位置到末位置的有向線段。其大小與路徑無關,方向由起點指向終點。它是一個有大小和方向的物理量,...
水平位移監測是指用觀測儀器和設備對水工建築物及地基有代表性的點位進行的水平方向位移量的量測。監測並分析水平位移的規律性,目的在於了解水工建築物在內、外...
物體或質點的位移是相對的,是指相對某一參考系而言,沒有參考系的位移是沒意義的。我們說的位移如果沒指明一般是以地球為參考系的也就是相對地球的位移。...
軸向位移又叫串軸,就是沿著軸的方向上的位移。總位移可能不在這一個軸線上,我們可以將位移按平行、垂直軸兩個方向正交分解,在平行軸方向上的位移就是軸向位移...
剛體平行移動(translation motion of rigidbody)剛體運動的形式之一指剛體上任一線段保持與其原位平行的運動.簡稱剛體平動...
靜態位移(static displacement)是由於地下淺層電性的不均勻,引起大地電磁測深曲線發生平行移動,而相應的相位曲線卻基本保持一致,這就是所謂的靜態位移。...
位移性技能基本類型 走,是身體重心從一隻腳到另一隻腳的移動過程,是身體的重量從一隻腳的腳跟到腳趾的自然滾動。走動時兩隻腳平行前行,腳趾向前,其中必須有一隻腳...
在研究物體運動過程中,某一時刻到另一時刻之間該物體的質心位移量的增加量成為位移增量。...
位移感測器又稱為線性感測器,是一種屬於金屬感應的線性器件,感測器的作用是把各種被測物理量轉換為電量。在生產過程中,位移的測量一般分為測量實物尺寸和機械位移兩種...
E光的位移量和晶體的長度成比例。 方解石晶體被組裝在一個表面作了黑色處理的銅質圓筒內。圖集 平行分束偏光稜鏡圖冊 V百科往期回顧 詞條統計 瀏覽次數:次 編輯...
散點透視及平行移動拼接拍攝法是指對對象的整體布局應進行全方位、多角度、細緻入微的科學考察和視覺研究,經過反覆斟酌,精心思考,最終確定切實可行的拍攝預案的方法...
平行縫焊機主要是套用於封裝積體電路晶片。現行階段,我國的封裝積體電路晶片的設備主要來自於美國和日本等已開發國家,價格十分昂貴,所以,使其能夠變得國產化,降低它的...
直線位移感測器的功能在於把直線機械位移量轉換成電信號。為了達到這一效果,通常將可變電阻滑軌定置在感測器的固定部位,通過滑片在滑軌上的位移來測量不同的阻值。...
磁致伸縮位移感測器,通過內部非接觸式的測控技術精確地檢測活動磁環的絕對位置來測量被檢測產品的實際位移值;該感測器的高精度和高可靠性已被廣泛套用於成千上萬的...
磁阻位移測量是近年來發展起來的一種新型位移感測器,它是利用磁敏電阻隨磁場強度大小的變化而引起阻值的改變來實現位移測量的。...
剛體內任一直線在運動過程中始終同原來位置保持平行的運動,又稱移動或平行移動。...... 剛體內任一直線在運動過程中始終同原來位置保持平行的運動,又稱移動或平行移...
平移泵是平行位移輸送泵的簡稱,也叫平行泵,最早由德國 Firstman 公司設計開發,專門套用於對剪下力高度敏感的物料的輸送。...
平行移動法 平行-順序移動法詞條標籤: 生活 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:10次歷史版本 最近更新: 創建者:yameilin...
