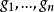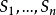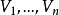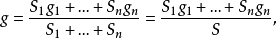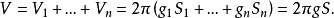基本介紹
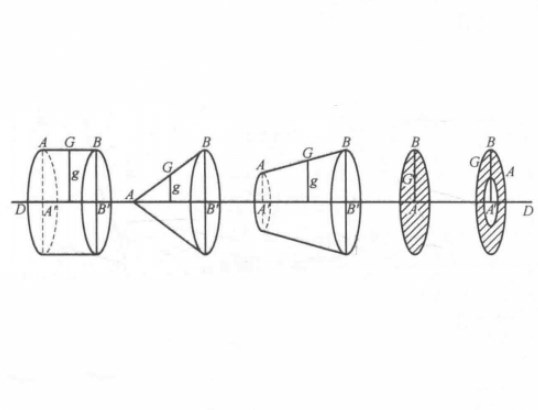
為了計算旋轉體的體積和表面積,亞歷山大的帕普斯(Pappus,公元三世紀末)給出一個法則,也叫帕普斯-古爾丁(Pappus-Guldin) 定理。這兩個定理是瑞士數學家
古爾丁1640 年發表的,但古希臘數學家帕普斯已經知道,帕普斯沒有給出證明,古爾丁給出了證明,但推理模糊不清,用現代思想首先證明的是義大利數學家卡瓦利里(Cavalieri)。他們的定理方便我們求旋轉面的面積和求旋轉體的體積,也可以幫助我們求弧線或面積的重心,
帕普斯表面積計算法則
帕普斯表面積計算法則也稱為帕普斯-古爾丁第一定理。
設一平面曲線位於這平面上一定直線D的一側,以D為軸將曲線旋轉360°,所產生的面積等於曲線長度和曲線的重心在旋轉中所畫的圓周長之積。
設l為曲線長,g為重心G到軸D的距離,S為旋轉面積,求
證明 第一步,設曲線為一條線段AB,設其端點在軸D上的射影為點A',B'(圖1),按AB與D的相關位置,有五種情況。
(1)旋轉面為圓柱面
S=2π·AA'·l= 2πgl.
(2)旋轉面為圓錐側面
S=π·BB'·AB=π·2g·l=2πgl
(3)旋轉面為稜台側面
S=π(AA'+ BB')·AB=π·2g·l= 2πgl.
(4)旋轉面為圓面積
S=π·AB2=π·2g·AB =2πgl.
(5)旋轉面為圓環
S=π(A'B2﹣A'A2)=π(A'B +A'A),
(A'B一A'A)=π·2g·l= 2πgl.
第二步,設曲線為折線AA
1A
2...A
n-1(圖2),設其各邊長為
,各邊重心距D為
,各邊旋轉面積為
,則折線的重心到D的距離為
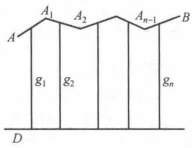 圖2
圖2由已證部分
第三步,對於任意曲線,作其內接n邊折線,設其旋轉面積為S
(n),重心距軸為)
,折線長為
,設n→∞且令每一邊趨於零,則
帕普斯體積計算法則
帕普斯體積計算法則也稱為帕普斯-古爾丁第二定理。設一平面區域在這平面上一定直線D的一側,以D為軸將圖形旋轉一周,則所產生的體積等於平面區域的面積乘以面積重心在旋轉中所畫的圓周長。
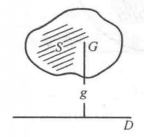 圖3
圖3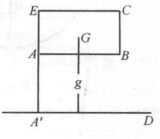 圖4
圖4設平面區域面積為S(圖3),面積重心G到D的距離為g,旋轉體積為V.求證
V = 2πgS.
證明 第一步,設平面區域為矩形ABCE(圖4),其兩邊與軸D平行.所產生的旋轉體積是兩個圓柱體積之差
V=π(A'E2-A'A2)AB
=π(A'E+A'A)·(A'E-A'A)AB
=π·2g·AE·AB
=2πgS
第二步,設平面區域由n個矩形區域組成,各個矩形有兩邊與軸D平行,設各矩形重心到D的距離為
,面積為
,所產生的旋轉體積為
,則
第三步,設平面區域是任意曲線圍成的,作其內接矩形使其各有兩邊與軸D平行,令矩形個數n→∞,並令每一矩形面積趨於零,取極限便得證明。
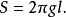
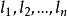
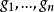
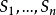
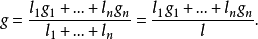
 圖2
圖2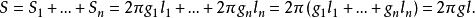
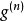
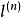
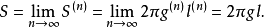
 圖3
圖3 圖4
圖4