希爾-吉田耕作定理

希爾-吉田耕作定理是給出某個C0類運算元半群生成元的充分必要條件的定理。

基本介紹

• 中文名：希爾-吉田耕作定理
• 外文名：Hille-Yosida theorem
• 適用範圍：數理科學

簡介

希爾-吉田耕作定理是給出某個C₀類運算元半群生成元的充分必要條件的定理。

希爾-吉田耕作定理是半群理論的最基本定理之一，它有多種表示形式。

內容

設A是巴拿赫空間X上的稠定線性運算元，則A是X上的某個C₀類運算元半群{T_t|t≥0}的無窮小生成元的充分必要條件是：存在常數M,β和實數列λ_n→+∞，滿足：

1、當λ_n>β時，(λ_nI-A)^-1是有界線性運算元；

2、對任何m，當λ_n>β時，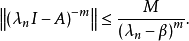

上述命題稱為希爾-吉田耕作（運算元半群）定理。

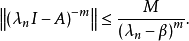
C0類運算元半群

C₀類運算元半群是一類具有強連續性的運算元半群。

設X是復的局部凸拓撲線性空間，L(X)表示X上的連續線性運算元全體。如果L(X)的運算元族{T_t|t≥0}滿足條件：

1、T_sT_t=T_s+t(s,t∈[0,+∞),T₀=I)；

2、（強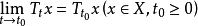），則稱{T_t|t≥0}為C₀類運算元半群，簡稱C₀類半群。

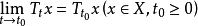
當X是巴拿赫空間時，對C₀類運算元半群{T_t|t≥0}必存在M>0和β≥0，使得||T_t||≤Me^βt(t≥0)。

例如X=L^p(-∞,+∞)(1≤p<+∞)，(T_tx)(ω)=x(t+ω)是C₀類（平移）運算元半群。這類運算元半群的理論主要是由希爾、吉田耕作和菲利普斯等人奠定的。