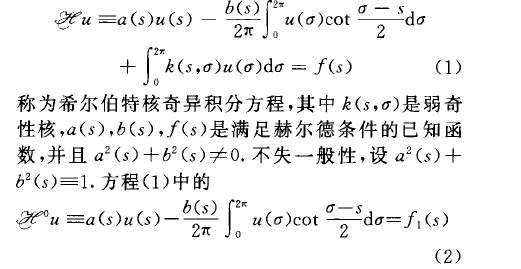
二,、.b fz}二,、』。一‘,
ulsJ=al is J.十- I J laJ}oi一一a a,
乙}Jo乙
a}S),b}S)不是常數時,特徵方程(2)可化為等價的希爾伯特邊值問題:a(s)u(s)+b(s)v(s)=Re[(a一ib)}(t)]
=f(s)(t=e").
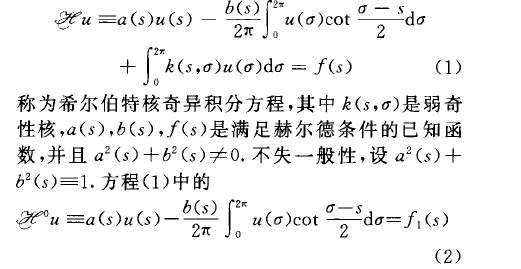
希爾伯特核奇異積分方程(singular integral e-quation with Hilbert kernel)一類重要的奇異積分方程.奇異積分方程 稱為(1)的特徵方程.整數‘=Ind[a(s)+ib(s)」...
弗雷德霍姆積分方程的重要推廣和發展,包括允許積分核有不可積的奇點,積分區間是無限區間等多種情形。使弗雷德霍姆定理不成立的線性積分方程,通常稱為奇異積分方程。...
對偶積分方程(dual integral equation)是一類重要的奇異積分方程,最重要的三類奇異積分方程是:1. 柯西核的奇異積分方程(包括希爾伯特核的奇異積分方程),這是研究得...
柯西奇異積分方程(Cauehy singular integral equations)是一類最基本且具有廣泛實際套用的奇異積分方程,其積分是柯西主值意義下的。柯西奇異積分方程與弗雷德霍姆積分...
(Fredholm)積分方程的弗雷德霍姆理論和奇異積分方程的諾特(Noether)理論以及逐次...此外,如下具有希爾伯特核的方程 也是一種主值意義下的奇異積分方程。對於這種...
高維奇異積分方程(singular integral equationin high dimension)希爾伯特變換在高維的推廣·與弗雷德霍姆積分方程不同,對於奇異積分方程,高維和一維是需要加以區別的....
(Fredholm)積分方程的弗雷德霍姆理論和奇異積分方程的諾特(Noether)理論以及逐次...對稱核積分方程的特徵值存在性,對稱核關於特徵函式序列的展開,以及希爾伯特 -...
廣義維納一霍普夫方程(generalized Wiener-Hopf equation) IL類主要奇異積分方程的統一名稱.多年來人們企圖用統一觀點去處理已經分別研究得相當深人的幾類主要的奇異...
他先後留學於英國劍橋大學和德國哥丁根大學,在羅素、哈代、希爾伯特等著名數學家...與天文學家霍普夫合作,共同研究一類給定在半無窮區間上的帶差核的奇異積分方程。...
在柯西型積分的表達式中,f(t)稱為它的核密度,1/t-z稱為柯西核。柯西核的奇異積分方程包括希爾伯特核的奇異積分方程,這是研究得最早和最完整的一類方程。...
全書共分12章,主要內容包括電彈性分析的基本理論和控制方程,均勻材料和裂紋體中...1.6 Riemann-Hilbert(黎曼一希爾伯特)問題1.7 Cauchy核奇異積分方程...
路見可,數學家。長期從事函式論領域的研究。主要成就涉及解析函式邊值問題,奇異積分方程理論、奇異積分方程數值理論和平面彈性的數學理論等領域。專長於函式論及其套用...
11·7 K(x,t)/|x-t|型無界核.奇異積分方程11·8 沃爾泰拉方程11·9 ...16·9 梅林變換.希爾伯特變換16·10 積分變換簡表第十七章 特殊函式17·1 Γ...
