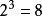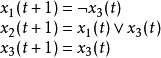布爾網路模型（Boolean Network，BN)最初是由Kauffman等提出，它是一種 以有向圖為基礎的離散系統。在布爾網路中，每個節點只有兩種狀態“開(on)” 和“關(off)”，而在某個時刻每個節點只能處於這兩種狀態中的某一種。每個節點下一時刻的狀態是由相鄰節點的狀態決定的，相鄰節點的狀態為輸入，經過一系列的邏輯運算得到本節點的新狀態。運算中使用的邏輯操作符包括:與（AND)、或(OR)、非(NOT)、異或(XOR)等。
布爾網路模型自提出以來一直受到人們的關注，並廣泛運用於包括細胞分化、免疫反應、生物進化、神經網路以及基因調控等在內的眾多領域。
基本介紹
- 中文名：布爾網路
- 外文名：Boolean Network
- 更新函式：布爾邏輯函式
- 取值範圍：0或者1
- 縮寫：BN
- 套用領域：系統生物學
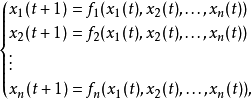
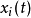
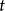
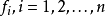
定義,性質,例子,
定義
布爾網路模型最早由Kauffman於1969年引入的，奠定了使用布爾網路研究基因調控網路的基礎。在布爾網路中,每個基因所處的狀態或者是“開”，或者是“關”。狀態“開”表示一個基因轉錄表達,形成基因產物，而狀態“關”則代表一個基因未轉錄。基因之間的相互作用關係由布爾表達式來表示。
簡單來說，布爾網路就是一系列相互作用的點，在每一個給定的時間，每個點只有兩個不同的值0和1，布爾網路的方程組形式：
性質
一、布爾網路的狀態演化
布爾網路的狀態演化是全局收斂的，也就是說無論從哪種初始狀開始演化，布爾網路的狀態總能進入某個狀態圈(或者不動點），系統將—直保持在這種狀態圈（或者不動點）統稱為吸引子(Attractor)，布爾網路系統進入吸引子狀態後，就具有一定的魯棒性，除非有外界的控制或者擾動，否則系統很難跳出吸引子狀態。所有能夠演化進入同一個吸引子狀態的轉台集合稱為這個吸引子的吸引域（Basin of the Attractor）。
布爾網路的狀態空間是由不同的吸引域組成的，系統的某一個狀態必定屬於某一個確定的吸引子和它的吸引域。所以處於吸引域中的狀態都稱為暫態(Transient state),處於吸引子的狀態稱為穩態（Stable State) 。
布爾網路的一個吸引子和它的的吸引域形成了一種狀態演化的樹型結構，吸引子是這棵樹的根，吸引域是這棵樹的樹幹和葉子，系統的狀態演化總是從“樹幹”狀態或者“葉子”狀態，進入“根”狀態。由於不同布爾網路會具有不同的拓撲結構或者不同的邏輯更新函式，所以它們的吸引子和吸引域都是不相同的。
二、布爾網路模型的優點
布爾網路雖然是一個理想化的簡化模型，但在基因系統中有著重要的套用。它提供了一個利用離散動力學過程來刻畫基因網路的表達模式的概念框架。用布爾網路來描述基因相互關係不需要具體的生化細節，
它提供了一個定性描述基因網路中的最根本的關係和從屬關係的工具。布爾網路的動力學過程的吸引子對應細胞的狀態，建立了吸引子的動力學過程與細胞狀態變化的關係。建立整體觀點下的基因功能，對細胞動態平衡和腫瘤的形成提供新的觀點。
三、布爾網路模型局限性
- 布爾網路是離散時間系統，它將每個基因點的狀態二值化，也將生物系統的狀 態進行了離散化的描述。然而在實際中，基因表達水平是一個連續值，所以要將基 因表達的數據離散化、二值化，但是這樣會造成信息的損失。同理，生物系統的狀 態演化也是連續的，對每個節點的離散化描述會造成整個系統信息的損失。而且當布爾網路的規模增大時，網路的狀態會以指數級增長，模型的複雜程度增加，模型對於生物系統描述的準確性也會大大下降。所以布爾網路 較為抽象的模型,它適合對系統進行巨觀的描述，在對準確性要求不高的情況下有較好的效果。Toussaim使用布爾網路模型構建了和人類老化相關的基因調控網路。
- 由於生物系統的隨機性，使得基因表達的過程中存在著大量噪聲和擾動，布爾網路這種確定性的模型不能準確描述基因間的調控關係。為了在布爾網路模型中引人不確定的因素，機率布爾網路（Probabilistic Boolean Networks,PBN)應運而生，它在原來節點之間關係的基礎上加入了機率模型。在機率布爾網路中節點的狀態演化可能根據多個布爾函式，基因採用哪個布爾函式進行演化，需要根據一定的機率來決定。因為有了多個更新函式，所以系統的計算量也隨之増大。
例子
右圖是一個三個基因節點的布爾網路，3個基因節點的布爾網路系統共有
個系統狀態。
其動態方程為
