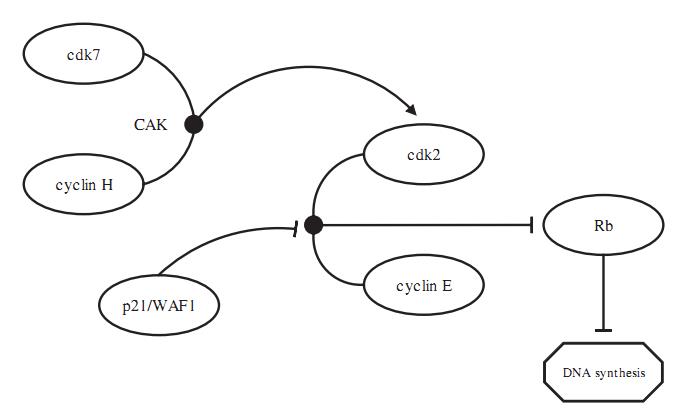
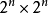機率布爾網路模型由Shmulevich等人於2002年提出，該模型是布爾網路模型的拓展。該模型中每個基因對應一個或多個布爾函式，每個疊代步驟中以一定機率選取其中一個函式預測其下一步的狀態。機率布爾網路保留了布爾網路的部分特性並且可以描述基因調控網路中的隨機現象。
機率布爾網為基因調控網路提供了一個更靈活的機率模型，以模擬生物系統中的不確定性。
基本介紹
- 中文名：機率布爾網、機率布爾網路
- 外文名：Probabilistic Boolean Network
- 縮寫：PBN
- 套用領域：系統生物學、布爾邏輯動力學系統
- 更新函式：布爾邏輯函式
- 相關概念：布爾網路
定義,例子,與布爾網路模型的異同,研究難點,
定義
機率布爾網路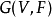
中包含一個節點集合
和一個布爾函式集合序列
。集合
中的
個布爾函式作為節點
的預測函式，
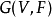
在每一步網路狀態轉移過程中，從集合 中以一定機率隨機選擇一個布爾函式作為節點
的預測函式，所有被選取的預測函式構成了一個函式向量
，該函式向量稱為
的一個實現(realization)。 的每個實現實際上都對應一個BN，因此可以看做是若干BN的機率組合。若每個節點預測函式的選擇是相互獨立的，則稱該為獨立的。獨立的包含的BN的個數為
若對所有
都與
，則BN的個數
，此時 退化為BN。
機率布爾網路的動態特性可用馬爾科夫鍊表述，其狀態轉移矩陣是一個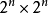
的矩陣，定義為
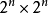
例子
假設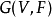 是一個包含三個節點的機率布爾網路，其中
，
，
，
，
，預測函式的真值表如表所示
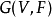
000 | 0 | 0 | 0 | 0 | 0 |
001 | 0 | 1 | 0 | 0 | 0 |
010 | 1 | 0 | 0 | 0 | 0 |
011 | 1 | 1 | 1 | 1 | 0 |
100 | 0 | 0 | 0 | 0 | 0 |
101 | 1 | 1 | 1 | 0 | 1 |
110 | 1 | 1 | 1 | 0 | 0 |
111 | 1 | 1 | 1 | 1 | 1 |
 | 1 | 0.6 | 0.4 | 0.6 | 0.4 |
該機率布爾網路包含八個狀態，其狀態之間的轉移關係如圖所示
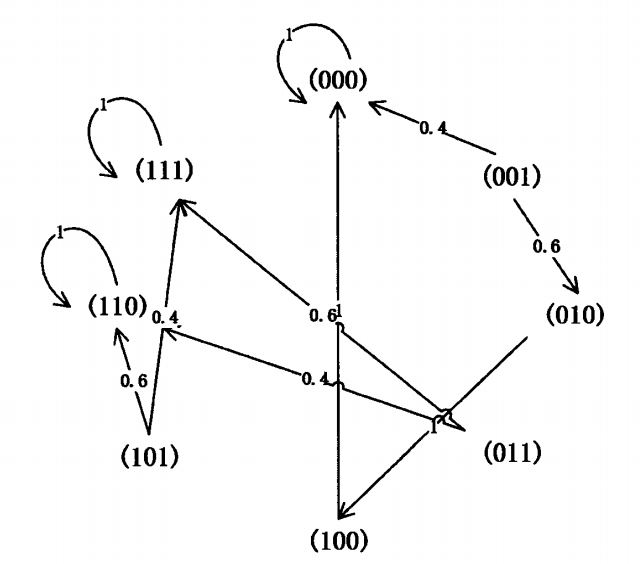
根據狀態轉移矩陣的定義可知，
與布爾網路模型的異同
- 機率布爾網路與布爾網路的狀態空間一致，大小均為2n；
- 布爾網路中任意狀態都唯一確定一個後續狀態，而機率布爾網路由於包含多個布爾網路，因此每個狀態可能對應多個後續狀態；
- 在布爾網路模型中，每個節點對應一個布爾函式，以該布爾函式作為其預測函式，布爾網路是一個決定性網路，網路當前狀態完全且唯一決定網路的下一步狀態。網路的狀態沿初始狀態在狀態空間中形成一條軌跡。由於狀態空間大小是有限的，這條軌跡最終將進入不動點或極限圈。而在機率布爾網路中，每個節點對應一個或多個預測函式，網路當前狀態可能對應多個後續狀態。
研究難點
機率布爾網路研究中的一個重要問題是求其馬爾科夫鏈相應的機率轉移矩陣，並計算該矩陣的穩態分布。機率轉移矩陣的穩態分布並不一定是存在的，為保證其穩態分布存在，可以在機率布爾網路中添加一個參數 。機率布爾網路中的節點狀態以機率 受控於其預測函式集，而以機率 隨機產生一個後續狀態。這樣，機率布爾網路的狀態是強連通的，從而保證機率轉移矩陣的穩態分布存在。
機率布爾網路的狀態轉移矩陣是一個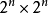的矩陣，當網路節點個數力很大時，求解其穩態分布很困難，因此如何簡化機率布爾網路模型是一個有意義的問題。目前機率布爾網路的一個簡化方法是忽略其中的一些小機率的布爾網路，其它的簡化方法還有待探索。
