布爾元(Boolean element)是布爾代數論域中元素的簡稱,常以字母a代表布爾代數論域B中的某個固定元素,且稱a為布爾常元或布爾定元;而以x代表B中任意一個元素,稱x為布爾變元。
基本介紹
- 中文名:布爾元
- 外文名:Boolean element
- 所屬學科:數學(布爾代數)
- 簡介:布爾代數論域中元素的簡稱
- 分類:布爾常元(布爾定元),布爾變元
基本介紹,相關說明,
基本介紹
1.交換律:
(1) a+b=b+a,
(2) a·b=b·a;
2.分配律
(1) a·(b+c)=a·b+a·c,
(2) a+b·c=(a+b)·(a+c);
3.0-1律
(1) a+0=a,
(2) a·1=a;
4.求補律
(1)a+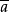 =1,
=1,
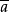
(2)a·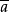 =0,
=0,
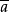
則稱代數系統(B,+,·,﹣,0,1)為一個布爾代數;稱三種代數運算“+”、 “·”、 “﹣”為布爾運算,稱B為布爾集,B中的元素稱為布爾元,0和1稱為布爾定元(或布爾常量),其餘的布爾元(如a,b,c,…)稱為布爾變元(或布爾變數),a+b稱為a,b的布爾和;a·b稱為a,b的布爾積,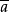 稱為a的布爾補。
稱為a的布爾補。
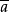
相關說明
上文布爾代數的定義採用的是公理化定義的方法,定義中(1)一(4)的運算律是作為原始公理給出的,並且由此構成的公理體系具有完備性(即所有的定理都可由它們推導出來)、獨立性(即其中無多餘的公理)、無矛盾性(即相互之間不能矛盾,並且由它們推導出來的定理也均不能矛盾)。
在布爾代數中,若B取作某一冪集P(S),兩個定元0,1分別看作空集∅和全集I,B上的三種布爾運算布爾加,布爾乘、布爾補分別看作集合的並、交,補運算。顯然,上面四條基本運算律成立,這時,布爾代數就成為集合代數,因此,集合代數是布爾代數的一個具體數學模型。
若取B=L={0,1},三種布爾運算規定如下:
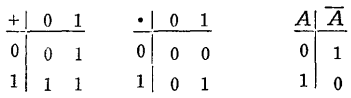
顯然, “+”、 “.”、 “﹣”是L上的代數運算,因此,<L,+,·,﹣,0,1>構成一個代數系統,容易驗證,它滿足布爾代數的四條基本運算律,故它是一個布爾代數,這種布爾代數叫二值布爾代數,二值布爾代數就稱為邏輯代數。

