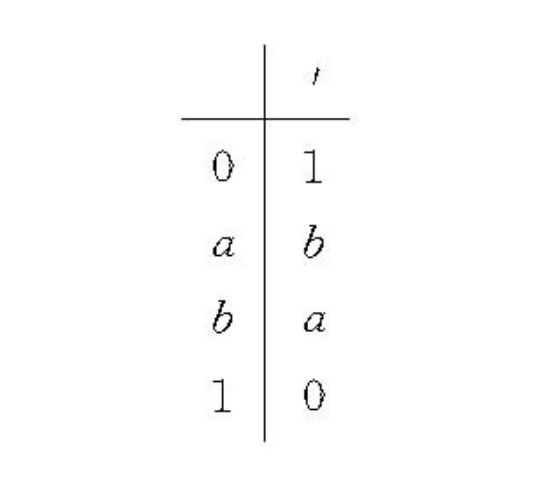布爾補

布爾補(Boolean complement)亦稱布爾否定(記為¬)或布爾余運算(記為—)，指布爾代數B=〈B，+，·，′，0，1〉中記為′的一元運算。對任意給定的一個元素a∈B，經補運算後得到一個確定的元素b∈B，b稱為a的布爾補，記為a′，即b=a′。

基本介紹

• 中文名：布爾補
• 外文名：Boolean complement
• 所屬學科：數學（布爾代數）
• 別稱：布爾否定，布爾余運算
• 簡介：一種一元運算

基本介紹

布爾取補運算用“—’’或“ ' ”表示，它是一種一元運算，其定義規則可按圖1規定，如=0，=1。

由取補運算所得的結果稱為布爾補，如=1可稱為0取補的布爾補為1。

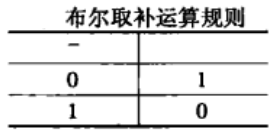圖1

布爾代數一般有以下三個概念。

1)布爾常量：布爾代數有兩個布爾常量，它們是0與1。

2)布爾變數：在域{0，1}上變化的變數稱為布爾變數，一般用x，y，z，…表示。

3)布爾表達式：由布爾常量、布爾變數通過布爾運算所組成的公式(包括括弧)，稱為布爾表達式。如(x+y)×z及x+(y×z×1)等均是布爾表達式。

布爾補的性質

布爾補滿足性質：a+a′=1，a·a′=0。

在元素不多的情形下，常可用列出補運算表來確定補運算，如含且僅含四個元素的布爾代數的補運算表就可列成右表，特別，對二元布爾代數，其布爾補運算是：1的補為0，0的補為1。

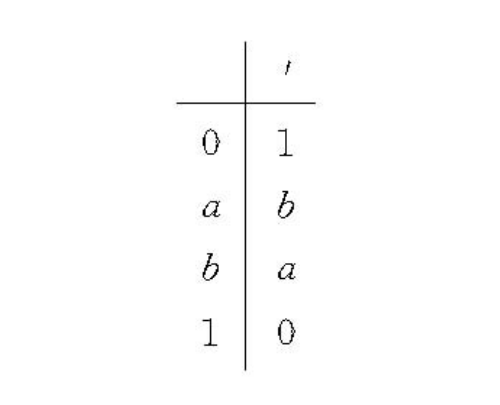圖2 布爾補

【例1】計算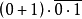的值。

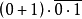
解：根據布爾和，布爾積，布爾補的運算規律得：