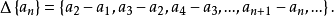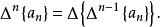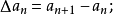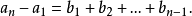差分數列是指由某個數列的差分構成的數列，給定數列a1，a2，…，an，…，記Δan=an+1-an，Δ2an=Δan+1-Δan，…，數列{Δan}∞n=1，{Δ2an}∞n=1，…分別稱為原數列{an}的一階差分數列，二階差分數列……an與Δak之間有下列關係：an=a1+∑n-1k=1Δak，類似地，Δan=Δa1+∑n-1k=1Δ2ak。這樣，如果某一階差分數列的部分和容易求出，就能求出通項an。
基本介紹
- 中文名：差分數列
- 外文名：Difference series
- 所屬學科：數學
- 簡介：由某個數列的差分構成的數列
基本概念,相關說明,公式,例題解析,
基本概念
由數列{an}的一階差分構成的數列稱為數列{an}的一階差分數列，記作Δ{an}或Δan，即
相關說明
對數列{an}有
，因此，如果能求得數列{an}的一階差分數列Δ{an}的前n-1項之和，即可求得數列{an}的通項公式。同樣可通過研究數列{an}的n階差分數列Δn{an}探求其n-1階差分數列Δn-1{an}的通項公式，從而最終求得{an}的通項公式，所以，研究數列{an}的差分數列是探求數列{an}的通項公式的途徑之一。
公式
一階差分：
二階差分：
......
n階差分：
例題解析
【例1】舉例說明什麼是差分數列、階差法。
解數列 -2 2 7 15 28 ......
一階差分 4 5 8 13......
二階差分 1 3 5...
三階差分 2 2...
像上面的例子那樣，從原數列各項分別減去它的前面一項，以所得的差為項，得到一個新數列，叫做原數列的一階差分數列；從一階差分數列各項分別減去它的前面一項，以所得的差為項的數列，叫做二階差分數列。如此類推，可得三階、四階、五階差分數列等。
利用上面這些差分數列的性質，可以求原數列的通項及前n項的和，這樣的方法叫做階差法。
注 一般地，對於數列
【例2】在數列2, 4, 8, 14,22, 32,...中:
(1) 以每相鄰兩項之差為項的數列，是怎樣的數列?
(2)求這個新數列的前n-1項的和。
(3)利用上面的結果求原數列的第n項。
解 (1)原數列的一階差分數列為2,4,6,8,10,...,這是一個等差數列，其首項a1=2,公差d1=2。
(2)
(3) 設原數列為{an}，差分數列內{bn}，則
將上列各式丙邊相加,得
