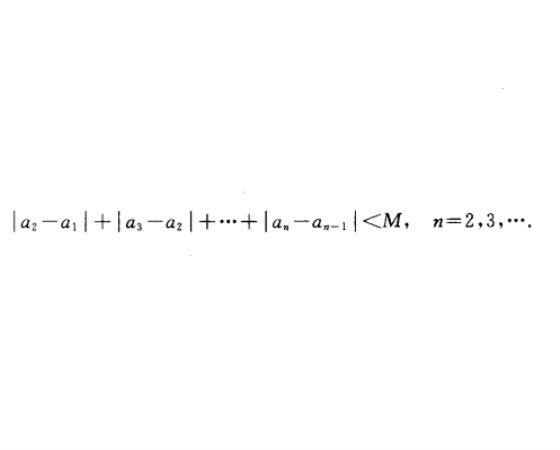有界變差數列

對於無窮數列{a_n}，如果存在常數C，滿足|a₂-a₁|+|a₃-a₂|+…+|a_n-a_n-1|<C 其中n=2，3，4，…，這樣的數列叫有界變差數列，凡有界變差數列必存在有窮極限，但反之不一定成立。

基本介紹

• 中文名：有界變差數列
• 外文名：Bounded variation sequence
• 所屬學科：高等數學（數學分析）
• 簡介：差分絕對值之和有界的數列

基本介紹

有界變差數列是一類重要的數列，指其差分絕對值之和有界的數列。對這樣的數列{x_n}，存在常數C，滿足：

|x₂-x₁|+|x₃-x₂|+…+|x_n+1-x_n|<C，

其中n=1，2，…有界變差數列必是收斂數列，但反之不一定成立。

有界變差數列必收斂

證明：有界變差數列必是收斂數列，但反之不一定成立。

分析令，利用單調有界原理證明數列{y_n}收斂，然後再利用柯西收斂準則證明數列{x_n}收斂。

證明 令。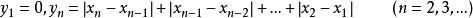

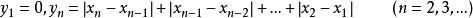
那么{y_n}單調遞增且有上界，所以{y_n}收斂。由柯西收斂準則，對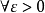，存在正整數N，當m>n>N時有，即

於是對數列{x_n}，當m>n>N時有

所以數列{x_n}收斂。

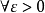
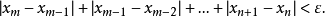
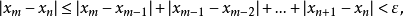
反之不一定成立，例如數列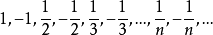，它是以0為極限的收斂數列，但它不是有有界變差的，事實上，

而數列是發散的，又是遞增的，所以，於是不是有界的。

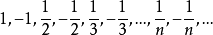
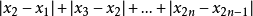
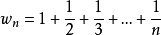
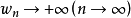
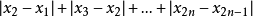
【例1】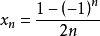

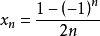
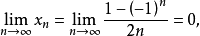
但

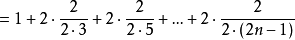
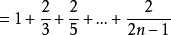
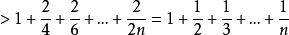
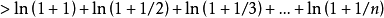
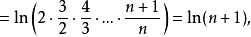
對任意c>0，只要n>e⁰就有>c，

數列{x_n}收斂，但它沒有有界變差。