基本介紹
- 中文名:
- 外文名:
- 所屬學科:
- 相關概念:
基本介紹,嶺估計,嶺跡法,其他k值確定方法,方差擴大因子法,疊代法,
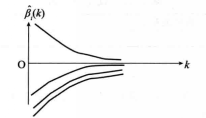
4) 在圖1(d)中, 和
和 都很不穩定,但其和卻大體穩定。這種情況往往發生在自變數
都很不穩定,但其和卻大體穩定。這種情況往往發生在自變數 和
和 的相關性很大的場合,即在
的相關性很大的場合,即在 和
和 之間存在多重共線性的情形,從選擇自變數的角度,兩者只保存一個就夠了。這種情況可以解釋某些回歸係數估計的符號不合理的情形,從實際觀點看,
之間存在多重共線性的情形,從選擇自變數的角度,兩者只保存一個就夠了。這種情況可以解釋某些回歸係數估計的符號不合理的情形,從實際觀點看, 和
和 不應有相反符號。
不應有相反符號。








5) 從全局看,嶺跡分析可用來估計在某一具體問題中最小二乘估計是否適用,把所有回歸係數的嶺跡都繪製在一張圖上,如果這些曲線比較穩定,如圖1(e)所示,利用最小二乘估計會有一定的把握。
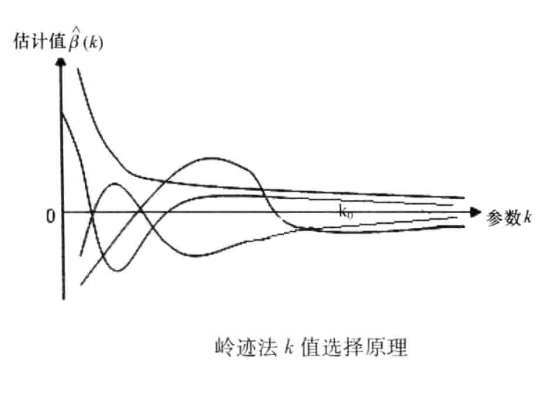
利用嶺跡法可以確定k,一般確定k需要遵循下面幾個原則:
1) 回歸方程各回歸係數的嶺估計基本穩定;
2) 用普通最小二乘法估計時,正負號表現出不合理的回歸係數,而利用嶺估計其符號變得合理,即嶺估計方法的使用改善了回歸方程參數估計的效果;
3) 回歸係數沒有出現不合理的符號;
4)估計量的精度沒有降低太多,即殘差項的平方和增大得不太多。
其他k值確定方法
下面僅針對嶺估計方法,介紹幾種常用的k值確定方法。
方差擴大因子法






此外,還可以根據Hoerl、Kernard和Baldwin(1975)提出的方法取k的固定值。具體確定方法如下:對於標準化的回歸模型





疊代法
疊代法是將上面計算的k的固定取值作為k的初始值,記為 ,然後建立回歸方程,估計回歸方程的參數,並計算新的k,即
,然後建立回歸方程,估計回歸方程的參數,並計算新的k,即 :
: