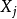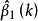基本介紹
在多重共線性下,由於
之間存在著較高的線性相關關係,導致
,因此構想給
加上一個正常數矩陣
,那么
接近奇異的可能性要比
接近奇異的可能性小甚至小很多,所以用
作為
的估計要比普通最小二乘法所得到的估計量穩定,這就是所謂的
嶺估計。
嶺估計方法的目的主要是減少
均方誤差,提高估計量的穩定性,但其缺點是估計量是有偏的。可以看到,k值越大,估計量的
方差就越小;同時,k的引入也會使最小二乘估計量的無偏性發生變化,變成有偏估計量,k越大,偏誤也就越大。而一個好的估計量應該是無偏的、方差最小的估計量,由於這兩個標準是相互矛盾的,因此k的確定就會變得很困難。到目前為止,雖然許多專家學者已提出多種確定k值的方法,但是,還沒有一種大家公認的、最優的確定k值的方法。
k值確定方法
下面僅針對嶺估計方法,介紹幾種常用的k值確定方法。
嶺跡法
嶺估計
的分量
作為k的函式,當k在
之間變化時,在平面直角坐標系中
所描繪的圖像稱為
嶺跡曲線。我們可以根據嶺跡曲線的變化形狀來確定適當的k。常用的嶺跡曲線及其顯示出的相關特點如下:
 圖1(a)
圖1(a)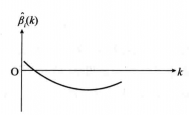 圖1(b)
圖1(b) 圖1(c)
圖1(c) 圖1(d)
圖1(d) 圖1(e)
圖1(e)1) 在圖1(a)中,
,並且比較大。這時可以將
看做是對Y有重要影響的因素。但
的圖形不穩定,當k從零開始略增加時,
顯著地下降,而且迅速趨於零,從
嶺回歸的觀點看,
對Y不起作用。
2) 與圖1(a)相反的情況如圖1(b)所示,
,但很接近零,這時
對Y的作用不大,但是隨著k略增加,
驟然變為負值,從嶺回歸觀點看,
對Y有顯著的影響。
3) 在圖1(c)中,
,說明
還比較顯著,但當k增加時,迅速下降,且穩定為負值,這時
是對Y有重要影響的顯著因素,從嶺回歸分析的角度看,
對Y有負影響的因素。
4) 在圖1(d)中,
和
都很不穩定,但其和卻大體穩定。這種情況往往發生在自變數
和
的相關性很大的場合,即在
和
之間存在多重共線性的情形,從選擇自變數的角度,兩者只保存一個就夠了。這種情況可以解釋某些回歸係數估計的符號不合理的情形,從實際觀點看,
和
不應有相反符號。
5) 從全局看,嶺跡分析可用來估計在某一具體問題中最小二乘估計是否適用,把所有回歸係數的嶺跡都繪製在一張圖上,如果這些曲線比較穩定,如圖1(e)所示,利用最小二乘估計會有一定的把握。
利用嶺跡法可以確定k,一般確定k需要遵循下面幾個原則:
1) 回歸方程各回歸係數的嶺估計基本穩定;
2) 用普通最小二乘法估計時,正負號表現出不合理的回歸係數,而利用嶺估計其符號變得合理,即嶺估計方法的使用改善了回歸方程參數估計的效果;
3) 回歸係數沒有出現不合理的符號;
4)估計量的精度沒有降低太多,即殘差項的平方和增大得不太多。
方差擴大因子法
在識別多重共線性時,我們了解了
方差擴大因子的概念,其可以用於度量多重共線性關係的嚴重程度,一般,當方差擴大因子>10時,模型的多重共線性關係就嚴重影響到估計量的質量。如果計算
的
協方差,得
則此式中矩陣
的對角元素
就是嶺估計的方差擴大因子。不難看出,
隨著k的增大而減少。套用方差擴大因子選擇k的經驗做法是,選擇使所有方差擴大因子
的k.這樣的k會使得嶺估計
相對穩定。
此外,還可以根據Hoerl、Kernard和Baldwin(1975)提出的方法取k的固定值。具體確定方法如下:對於標準化的回歸模型
其中,
為
時回歸模型參數的最小二乘估計,
為回歸方程的殘差均方。
疊代法
疊代法是將上面計算的k的固定取值作為k的初始值,記為
,然後建立回歸方程,估計回歸方程的參數,並計算新的k,即
:
按同樣的方法,用
計算
,重複這一過程,直到
的前後兩個估計值之間的差異不是很明顯為止。





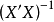





 圖1(a)
圖1(a) 圖1(b)
圖1(b) 圖1(c)
圖1(c) 圖1(d)
圖1(d) 圖1(e)
圖1(e)