基本介紹
- 中文名:尼德曼-翁施算法
- 外文名:Needleman-Wunsch Algorithm
歷史與算法發展,尼德曼-翁施算法簡介,初始化得分矩陣,選擇得分體系,填充得分矩陣,得分體系,基礎得分標準,相似度矩陣,間隔補償,進階矩陣,程式代碼,套用,三維立體畫,電腦立體視覺效果,
歷史與算法發展
通過Needleman和Wunsch的描述的算法的最初目的是找到在兩種蛋白質的胺基酸序列的相似性。Needleman和Wunsch的描述他們的算法為明確的情況下,當對準被匹配和不匹配僅僅懲罰,並差距沒有懲罰(D =0)。從1970年最初發布提示遞歸。

一個更好的動態規划算法二次運行時間為同樣的問題(無間隙罰款)最早是由大衛Sankoff1972年類似的二次時間算法推出了由TK Vintsyuk於1968年獨立發現了一種語音處理(“時間扭曲”),由羅伯特·華格納和麥可·J·菲舍爾在1974年的字元串匹配。Needleman和Wunsch的配製最大化相似性的問題。另一種可能性是最小化序列之間的編輯距離,弗拉基米爾的Levenshtein引入。彼得·塞勒斯在1974年發現的兩個問題是等價的。Needleman-Wunsch算法仍是廣泛使用的最佳全局比對,特別是當全局比對的質量即結果是最重要的。然而,該算法是相對於時間和空間的昂貴,正比於兩個序列,因而不適合長度特別長的序列比對。
最近的發展一直專注於提高算法的時間和空間成本,同時保持質量。例如,在2013年,快速最佳化整體序列比對算法(FOGSAA),建議比其他最佳全局比對的方法,其中包括中的Needleman-Wunsch算法更快核苷酸/蛋白質序列的比對。紙張聲稱相比中的Needleman-Wunsch算法時,FOGSAA達到70-90%為高度相似核苷酸序列的時間增益(具有>80%的相似性),並且對於具有30-80%的相似性的序列54-70%。
全局性配對和局部性配對的比較全局性配對和局部性配對的基本區別是在局部性配對中,你將嘗試用你訴求的序列的片段或局部來進行配對。而在全局性配對中,你將嘗試使用整個序列(從起始端到結束端)來進行配對,也即是說,在全局性配對中,當你的比對序列長度不一致時,在配對過程中可能會產生間隔或者不匹配的情況。注意,在局部性配對中也有可能產生間隔。
局部性配對:

全局性配對:

在Needleman-Wunsch(全局性)算法中,分數跟蹤系統是基於得分矩陣的右下角開始的。然而在Smith-Waterman(局部性)算法中,得分矩陣的起始點是基於分數最高的坐標位置。 全局性配對主要套用於比較同源性的基因的相似性而局部性配對主要套用於在非同源性的基因序列中尋找具有相似性的同源的基因域。
尼德曼-翁施算法簡介
有序列: GCATGCU
GATTACA
初始化得分矩陣
首先建立如圖一的得分矩陣。從第一列第一行的位置起始。計算過程從d 0 , 0開始,可以是按行計算,每行從左到右,也可以是按列計算,每列從上到下。當然,任何計算過程,只要滿足在計算d i , j時d i-1 , j、d i-1 , j-1和d i, j-1都已經被計算這個條件即可。在計算d i , j後,需要保存d i , j是從d i-1 , j、d i-1 , j-1或di, j-1中的哪一個推進的,或保存計算的路徑,以便於後續處理。上述計算過程到d m , n結束。
選擇得分體系
接下來我們需要決定如何給每個獨立配對打分。從我們的序列中,你可能就能發現最好的序列配對之一:
GCATG-CU
G-ATTACA
- 匹配: 兩個字母相同
- 不匹配:兩個字母不相同
- 錯位:一個字母與另一個序列中的間隔(空白)相匹配
這三種得分情況有很多打分標準,這些情況都總結在得分體系的部分。我們將使用Needleman 和Wunsch創造的簡單體系來進行打分,即匹配得一分,不匹配得-1分,錯位得-1分.
填充得分矩陣
開始於第二行中的第二列,初始值為0。通過矩陣一行一行移動,計算每個位置的分數。得分被計算為從現有的分數可能的最佳得分(即最高)的左側,頂部或左上方(對角線)。當一個得分從頂部計算,或從左邊這代表在我們的對準的插入缺失。當我們從對角線計算分數這表示兩個字母所得位置匹配的對準。定不存在“向上”或“左上”的位置對第二行,我們只能從現有單元向左添加。因此,我們添加-1的權利,因為這代表了從以前的比分插入缺失。這導致在第一行是0,-1,-2,-3,-4,-5,-6,-7。這同樣適用於第二列,因為我們只具有以上現有分數。因此,我們有:

所以根據該矩陣就可以方便的求出匹配路徑:
根據該矩陣就可以方便的出我們想要的匹配路徑了。 結果: 序列最佳匹配 --------- ---------------------- GCATGCU GCATG-CU GCA-TGCU GCAT-GCU GATTACA G-ATTACA G-ATTACA G-ATTACA 匹配: +GCATGCU +GATTACA |
得分體系
基礎得分標準
最簡單的打分體系只考慮匹配,不匹配與間隔三種情況。在新手指南中使用的打分體系是匹配=1,不匹配=-1,間隔=-1。在這種情況下序列越長,得分越低,在本體系中我們期望好的匹配取得高分。另一種打分體系如下:
- 匹配=0
- 間隔=1
- 不匹配=1
在本體系中得分將會代表兩序列中匹配的距離。不同的得分體系適用於不同的情況。例如,如果在你的匹配中間隔被認為有很大的負面影響,你可以使用間隔扣分很多的打分體系:
- 匹配=0
- 間隔=10
- 不匹配=1
相似度矩陣
更複雜的打分體系不僅僅考慮選擇的不同類型,也考慮每個不同的字母的影響。例如,字母A與A匹配將得到4分。為了表示所有字母匹配得分的情況,我們將會使用相似度矩陣來幫助計算。
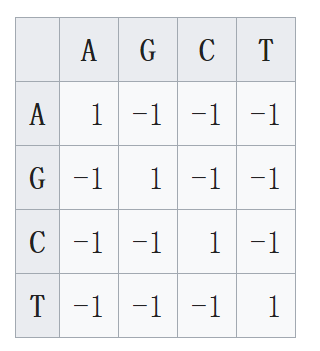
每個分數代表從一個字母轉換到下一個位置的所有可能的情況的得分。
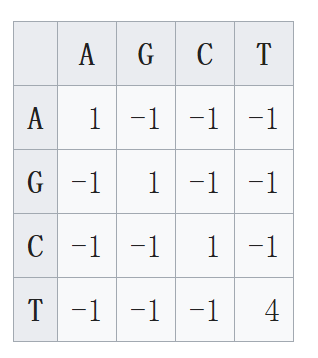
不同的得分矩陣適用於不同的情況。該得分體系對於蛋白序列的匹配比對尤為重要。以下為兩種廣為引用的蛋白序列相似度矩陣
- BLOSUM
間隔補償
當比對序列往往存在差距(即插入缺失),有時路數。生物學上,有很大的差距更容易,而不是多個單一缺失的發生為一體的大型刪除。因此,我們應該進球兩個小的插入缺失是有過之而無不及一個大的。簡單和常見的方式做,這是通過一個大的差距,比分開始一個新的插入缺失和一個較小的間隙延伸得分為每個擴展了插入缺失信。例如,新插入缺失可能會花費-5和擴展,插入缺失可能會花費-1。
進階矩陣
例如,如果相似度矩陣如下圖1所示:
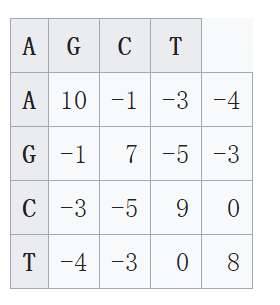
圖1
那么匹配結果如下:
AGACTAGTTAC
CGA----GACGT
如果間隔懲罰因子是-5,那么該匹配的得分為:
S(A,C) + S(G,G) + S(A,A) + (3 × d) + S(G,G) + S(T,A) + S(T,C) + S(A,G) + S(C,T)
= -3 + 7 + 10 - (3 × 5) + 7 + (-4) + 0 + (-1) + 0 = 1
計算序列相似程度時還應該考慮序列長度的影響。令S(s, t) 表示兩條長度分別為m和n的序列的相似性得分,假設S(s, t) = 99,兩條序列有99個字元一致。如果 m=n=100 ,則可以說這兩條序列非常相似,幾乎一樣。但是,如果m=n=1000,則僅有10% 的字元相同。所以,在實際序列比較時,使用相對長度的得分就更有意義,定義: (4) 以sim(s,t)作為衡量序列相似性的指標。 從所使用的數據結構d i , j本身及其計算過程來看,序列兩兩比對基本算法的空間複雜度和時間複雜度都是O (mn)。如果兩條序列的長度相近,空間和時間複雜度就為O (n2)。
程式代碼
本算法可以在多個平台上實現運算,常見的程式語言均有公開的代碼可以參考使用。
OPTIONS:
--file <file> 同時讀取比對的兩序列檔案
--files <f1> <f2>
--stdin 讀取標準檔案頭
--case_sensitive 使用大小寫字母區分
--match <score> [默認: 1]
--mismatch <score> [默認: -2]
--gapopen <score> [默認: -4]
--gapextend <score> [默認: -1]
--scoring <PAM30|PAM70|BLOSUM80|BLOSUM62>
--substitution_matrix <file>
--substitution_pairs <file>
freestartgap 間隔不扣分 freeendgap 序列結束不扣分
printscores 列印最佳化後的比對分數 zam printmatrices 列印動態矩陣 printfasta 列印fasta格式的檔案頭 pretty 列印描述行 colour 列印顏色
可選最佳化項:
nogapsin1 被比對序列不允許有間隔
nogapsin2 比對序列不允許有間隔
nogaps 所有序列均不允許有間隔
nomismatches 不允許有誤差配對
套用
三維立體畫
三維立體畫是利用人眼立體視覺現象製作的繪畫作品。普通繪畫和攝影作品,包括電腦製作的三維動畫,只是運用了人眼對光影、明暗、虛實的感覺得到立體的感覺,而沒有利用雙眼的立體視覺,一隻眼看和兩隻眼看都是一樣的。充分利用雙眼立體視覺的立體畫,將使你看到一個精彩的世界。人有兩隻眼,兩隻眼有一定距離,這就造成物體的影象在兩眼中有一些差異,見右圖,由圖可見,由於物體與眼的距離不同,兩眼的視角會有所不同,由於視角的不同所看到是影象也會有一些差異,大腦會根據這種差異感覺到立體的景象。三維立體畫就是利用這個原理,在水平方向生成一系列重複的圖案,當這些圖案在兩隻眼中重合時,就看到了立體的影象。參見下圖,這是一幅不能再簡單的立體畫了。圖中最上一行圓最遠,最下一行圓最近,請注意:最上一行圓之間距離最大,最下一行圓之間距離最小。重複圖案的距離決定了立體影象的遠近,生成三維立體畫的程式就是根據這個原理,依據三維影象的遠近,生成不同距離的重複圖案。 立體畫有兩種形式:第一種是由相同的圖案在水平方向以不同間隔排列而成,看起來是遠近不同的物體。 另一種立體畫較複雜,在這種立體畫上你不能直接看到物體的形象,畫面上只有雜亂的圖案,製作這樣的立體畫只有使用程式了。兩種作品看法是一樣的,原理都是使左眼看到左眼的影象,讓右眼看到右眼的影象。
