基本介紹
- 中文名:導出偶
- 外文名:derived couple
- 所屬學科:微分拓撲
- 提出者:馬西(W.S.Massey)
- 別名:導出正合偶
- 相關概念:正合偶,雙分次模,正合列等
定義
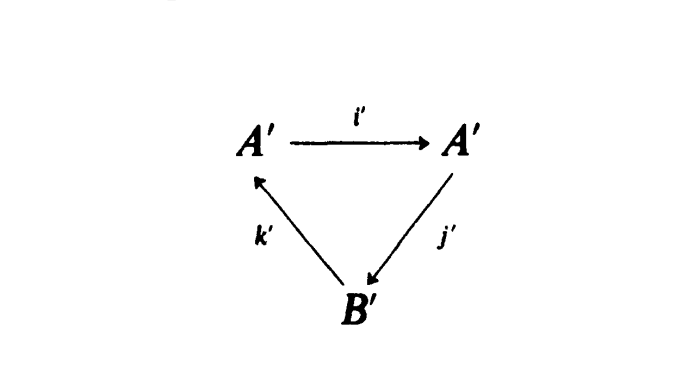
基本介紹
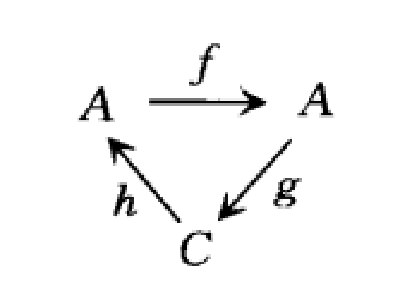













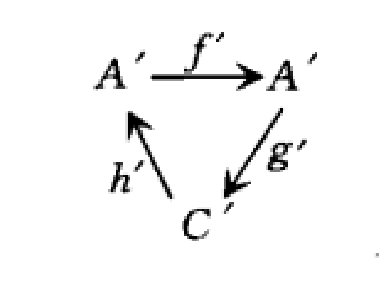

相關介紹
正合偶


























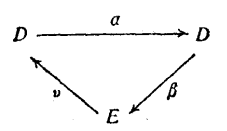












































導出偶又稱導出正合偶,是譜序列理論中一個與正合偶相關的概念,正合偶是由兩個雙分次模所組成的正合三角形,它是馬西(W.S.Massey)提出的,是譜序列理論一個重要概念。由正合偶可得出其導出偶,且由此可得出譜序列。定義設(...
導出設計(derived design)是一種重要的設計,指由對稱設計導出的平衡不完全區組設計。基本介紹 導出設計的具體構作方法如下:若一個 的區組為 ,取定其中一個區組B,對其餘區組 ,記 ,且 ,則 是一個 ,稱這個設計為原對稱設計...
並證明了d-Koszul代數上的廣義d-Koszul模的偶次上同調群構成一個Koszul模,由此證明了d-Koszul代數上d-Koszul模的奇次上同調為Koszul模,肯定回答了Green等04年(J Pure Appl Alg)提出的一個問題;證明了代數的有界導出範疇與完備復...
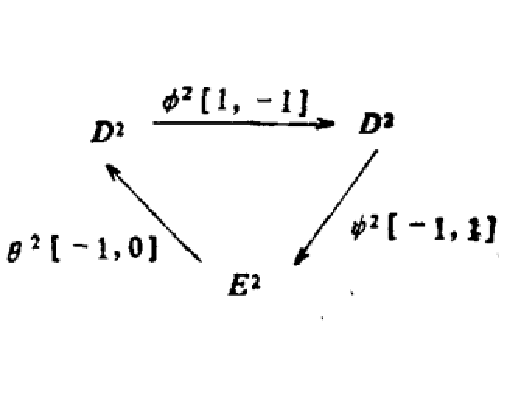
,一個正合偶是:一對對象 三個態射: 使之滿足下述正合條件:將這組資料簡記為 。正合偶通常以三角形表示。 對應到譜序列的 項,而 是一些輔助資料。為了得到譜序列的後續項,以下將構造導出偶。令:由 導出。定義如下...
在數學中,雙曲函式是一類與常見的三角函式(也叫圓函式)類似的函式。最基本的雙曲函式是雙曲正弦函式sinh和雙曲餘弦函式cosh,從它們可以導出雙曲正切函式tanh等,其推導也類似於三角函式的推導。雙曲函式的反函式稱為反雙曲函式。雙...
該AD596 是一款單晶片溫度設定點CON-控制器經過最佳化用於在高溫下如在烘箱中的控制套用中。該裝置冷端補償和放大, J或K型熱電偶耦合輸入導出內部信號正比於溫perature 。內部信號,然後與外部相比施加的設定點電壓,以產生一個低阻抗的...
熱流是溫度的導出量,它的測量熱量轉移的儀器稱之為熱流計或熱流傳遞的熱量。其單位為W/CM2.溫度指示和調節儀 在科研生產過程中,為了獲得測量數據,保證生產過程的正常進行,必須對相關的溫度,壓力,流量等參數進行測量,並將測量結果指示...
