基本介紹
- 中文名:姿態計算
- 外文名:attitude calculation
- 套用:航空航天飛行器
- 方法:方向餘弦矩陣、四元數等
- 一級學科:航空航天科技
- 二級學科:航空航天原理
相較區別
內容介紹
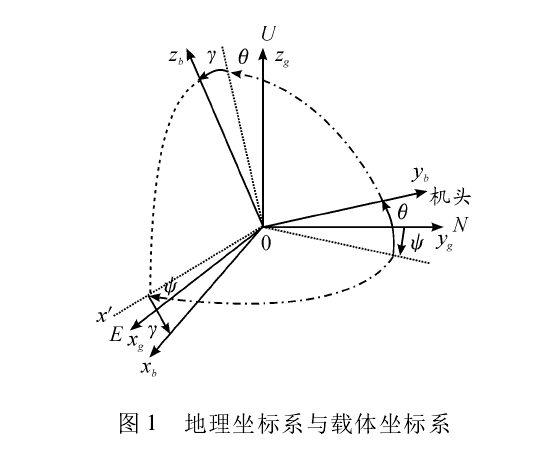

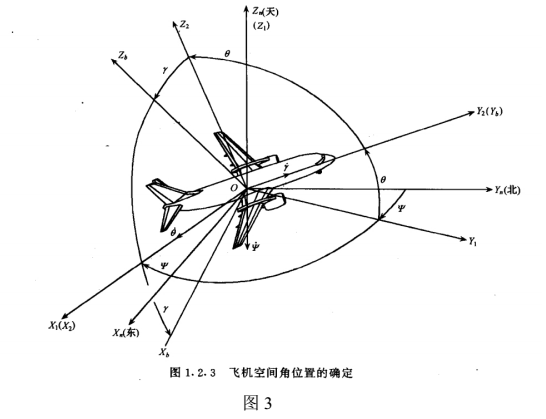


在GINS中,姿態是通過環架上的角度感測器敏感的,無需計算,而在SINS中,所有的導航計算(位置、速度、姿態)都要通過計算得出,而且姿態計算(attitude calculation)的頻率最高。關於姿態計算最為常用的方...
《姿態控制計算機總結》是一款IOS平台的套用,支持iOS5.0及以上版本。套用介紹 資金是新的超級直觀的手勢控制計算機。 使數學快速簡單和有趣! 總結了使用多個手勢像花瓣使執行數學操作更快、更多的病人就檢查的任務比標準計算器。 與大...
基於模型的姿態估計方法是通過比對真實圖像和合成圖像,進行相似度計算更新物體姿態。基於模型的方法為了避免在全局狀態空間中進行最佳化搜尋,一般都將最佳化問題先降解成多個局部特徵的匹配問題,非常依賴於局部特徵的準確檢測。當噪聲較大無法提取...
航天姿態控制計算機是對航空器姿態控制系統進行計算的計算機系統,其主要功能是接受敏感器傳遞過來的姿態信息,經過計算後將控制信息傳遞給執行機構,實現控制規律或控制對策,從而完成對太空飛行器的控制任務。主要功能 噴氣三軸姿態 利用各種推力...
(1)研究三維空間的不變性特徵,用於姿態變化中的人體部位描述及跟蹤;(2)設計基於三維空間的部位遮擋識別及其恢複方法,用於解決由遮擋引起的姿態估計錯誤問題;(3)探索複雜場景中基於圖結構的人體姿態估計方法,用於實現多樣化人體姿態...
將頭部運動建模為繞頸部固定點的旋轉運動,通過計算旋轉角度來實現頭部姿態角度的測量;通過頭部模型和三自由度轉台相結合的實驗來進行頭部姿態估計方法的驗證,建立科學的誤差模型,揭示提高頭部姿態估計精度的一般性規律。
利用分級GPLVM(HGPLVM, Hierarchical GPLVM),對人體的各肢體部分分別學習GPLVM模型,再進行姿態估計,比起僅進行整體GPLVM模型學習,估計效果會更好。 (3)研究了基於隨機梯度下降(Stochastic Gradient Descent)對GPLVM模型最佳化的算法,以及...
最佳化的姿態參數重構算法適於節點自處理,以提高系統實時性。硬體平台體積小,功耗低,具有數據採集,無線控制及傳輸,姿態參數重構自處理的功能,可實時獲得關節自由度參數。進而利用計算量極小的多剛體正向運動學進行實時建模。鑒於以上特點,...
1. 以高斯過程隱變數模型為基礎,針對狀態方程、觀測方程以及低維隱變數動態方程中的參數同時進行邊緣化積分輸出一個最小化的目標函式,從該目標函式出發,研究共享動態隱變數模型的解析表達;採用主分量分析(PCA)方法計算出高維狀態和觀...
2.測量方法: 受試者可以選擇站立(靜態測試)或跑台行走測試(動態測試),裸露背部,由掃瞄器進行持續5秒左右的掃描記錄,系統再進行自動計算和形狀識別來進行建模。 3.測量時間: 每名受試者測試時間總體在10分鐘左右。 4.測量點參數...
(1)在搭建形狀感測系統的基礎上,提出局域互相關方法,解決傳統互相關計算存在多峰偽峰問題。該方法摒棄了使用整段頻譜進行互相關的傳統方法,採用基於局部頻譜更為相似的原理,計算局部頻譜的歐氏距離,然後根據此距離來判斷波長漂移值。
研究運行姿態的頻譜結構、能量或強度隨時間變化的特徵,結合姿態空間概念及其動力學性質,預測系統動力行為的變化趨勢;研究提出通過計算分析姿態信號對抗含頻率自變數邊界約束條件的程度,量化評價高速運行的安全性和平穩性;研究依據姿態信號時...
依靠中國國外的自動導向測量系統進行盾構機姿態覆核,費用高昂,成本高,2016年12月之前的人工測量方法存在精度低、測量計算占用時間長等缺點。發明內容 專利目的 《一種用於隧道施工的盾構機姿態覆核方法》提供一種用於隧道施工的盾構機姿態...
5)利用來自多個周期T0的有效載荷觀測數據和星敏感器測量數據,將其等效到一個周期T0內,從而使得所述每個時間段中數據對數量N增加,返回3)、重新計算星敏感器基準偏差估計值。一種利用星敏感器對有效載荷基準偏差進行估計和修正的方法,...
在這種模式下,雙基準平行光源的兩路平行光線經針孔光闌,成像在CMOS圖像感測器件上,通過針孔光斑圖像中心在成像面上的位置,計算出入射的平行光線與探測器基準軸線之間的夾角,基於雙矢量定姿原理,完成三維姿態角的測量。
然後在陽照區使星體繞Z軸以某一角速度轉動,偏航太陽敏感器將搜尋太陽,當太陽處於偏航太陽敏感器視場之內時,依照偏航太陽敏感器的輸出,即可計算出此時星體的偏航姿態,控制星體使偏航姿態達到給定值,即完成偏航捕獲。中國返回式衛星用此...
獲得的主要研究成果如下:(1)針對複雜衛星姿態確定系統,系統分析了基於EKF姿態確定方法的精度影響因素,研究了包括敏感器測量精度、敏感器相對安裝誤差及初始估計精度等11種因素對姿態確定精度的影響,根據試驗設計安排試驗,計算不同因素...
IMU輸出原始數據,然後通過慣性導航算法得出儀器在管道內穿行過程中的自身三軸姿態角(或角速度)、當前加速度。里程輪記錄行進里程。通過積分算法對這些姿態量進行分析和計算以最終獲得管道的三維姿態。產品特點 1.坐標精確連續 2.不受埋...
協調操縱駕駛桿和腳蹬,偏轉副翼和方向舵,產生滾轉力矩和偏轉力矩,以達到控制側向姿態的目的。通過飛行姿態控制系統(飛行自動控制系統中的一個子系統)來實現。飛行姿態控制系統一般由姿態敏感元件、綜合計算裝置、信號給定裝置和執行機構等...
陀螺儀輸出角速度,是瞬時量,角速度在姿態平衡上是不能直接使用, 需要角速度與時間積分計算角度,得到的角度變化量與初始角度相加,就得到目標角度,其中積分時間Dt越小,輸出角度越精確,但陀螺儀的原理決定了它的測量基準是自身,並沒...
(2)姿態控制執行機構。用以產生控制力矩以糾正姿態誤差,達到期望的姿態。(3)計算機或控制器。用以實現控制律,即從姿態信息計算出控制指令,輸入到執行機構,產生期望的控制力矩以消除姿態誤差。方案選擇 方案選擇是指系統控制規律及實現...
(4)計算量不同。平台慣導中,平台以物理實體形式存在,平台模擬了導航坐標系,運載體的姿態角和航向角可直接從平台框架上拾取或僅通過少量計算獲得。但在捷聯慣導中,平台並不實體存在,而以數學平台形式存在,姿態角和航向角都必須經過...
此外,通過使用對偶四元數建立了不同衛星坐標系與慣性坐標系之間的坐標變換關係,進一步將姿態與軌道信息統一處理,可最佳化系統模型,明顯減少計算量。在建立編隊衛星力學模型的基礎上,將深入研究三種基於對偶四元數的軌道和姿態確定算法,並...
