基本介紹
- 中文名:奇異系統
- 外文名:singular systems
- 研究始於:20世紀70年代初
- 別稱:描述變數系統或半狀態系統。
- 包括:慢變子系統、快變子系統
- 描述方法:微分方程、差分方程、代數方程
奇異系統簡介
奇異系統的分類
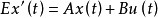
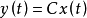
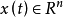
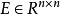
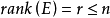
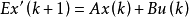
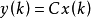
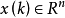
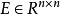
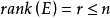
典型的奇異系統
Leontief經濟模型
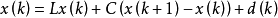
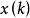
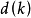
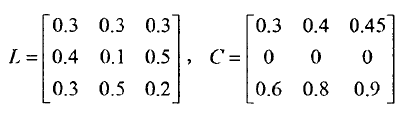
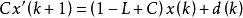
神經網路模型
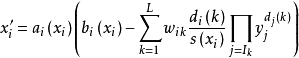
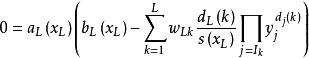
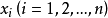
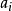
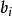
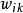
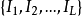
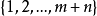
Hopfield神經網路模型
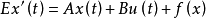

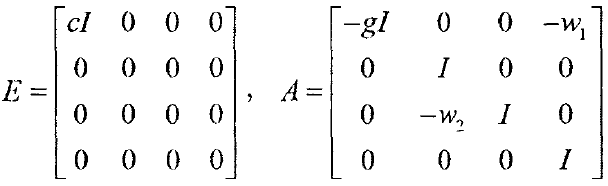
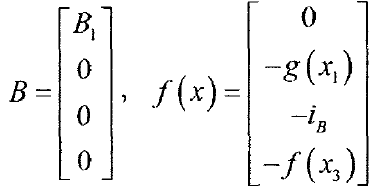
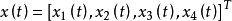
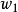
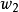
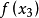
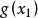

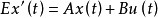
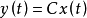
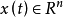
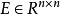
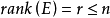
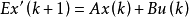
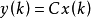
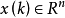
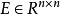
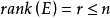
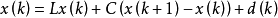
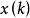
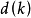
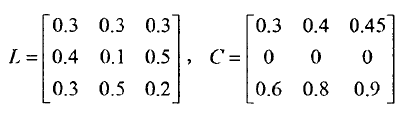
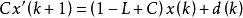
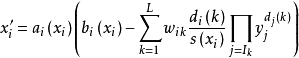
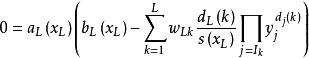
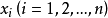
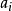
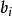
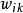
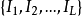
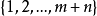
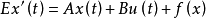

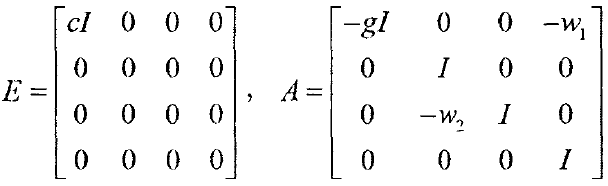
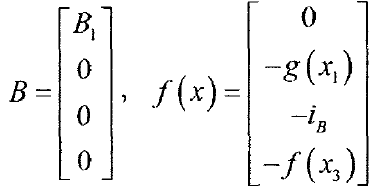
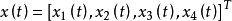
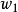
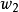
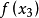
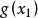
奇異系統,又稱廣義狀態空間系統、描述變數系統或半狀態系統。奇異系統是一類比正則系統具有更廣泛適用度的系統描述形式,包含微分方程(連續系統)或差分方程(離散系統)...
線性系統是指同時滿足疊加性與均勻性(又稱為其次性)的系統。奇異系統是一類由微分及代數方程綜合描述的系統,它在結構形式上比僅由純微分方程或差分方程描述的正則...
非線性系統,指的是系統的狀態與輸出變數在外部條件的影響下,不能用線性關係來描述的系統。奇異系統是一類由微分及代數方程綜合描述的系統,它在結構形式上比僅由純...
《2-D奇異系統理論》結合作者多年的研究工作,系統地總結了2、D奇異系統的基本理論、研究方法和近年來所取得的主要研究成果,引導讀者進入該領域的研究前沿。《2-D...
本書主要介紹非線性奇異系統研究的最新理論成果及其套用,包括非線性奇異系統的工程背景、結構特徵和數學準備知識;非線性奇異系統的正則性與正則化問題;非線性奇異系統...
奇異系統是一類由微分及代數方程綜合描述的系統,它在結構形式上比僅由純微分方程或差分方程描述的正則系統多了代數方程描述部分。奇異系統也被稱為流形上的微分代數...
奇異Hamiltonian系統周期解論文作者是張後揚,導師是陳文〓教授...... 奇異Hamiltonian系統周期解論文作者是張後揚,導師是陳文〓教授 副題名外文題名The Periodic ...
1)付主木, 費樹岷. 一類不確定切換奇異系統的動態輸出反饋魯棒H∞控制[J]. 自動化學報,2008, 34(4): 482-487.2)付主木, 費樹岷, 叢屾. 一類切換線性奇異...
主要從事網路控制理論和套用研究,奇異系統、量化反饋系統的魯棒控制、非線性控制、先進過程控制和信息融合。研究內容:系統的建模、分析、最佳化、調度與控制。2017年4月...
離散雙曲系統的共軛分類結果,發展了“嵌入流”方法,拓廣了特徵值和譜的旋轉數方法,闡述了低自由度Lagrange系統的周期運動的扭轉性和穩定性,並在奇異系統的周期邊...
