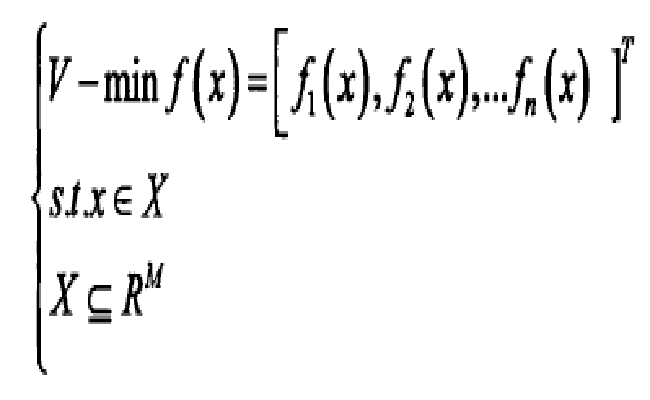多目標控制指的是同時控制兩個或多個相互依賴的目標，並且是時域性能和頻域性能的混合控制。
控制系統的多目標最佳化設計一直是人們致力研究的課題，比如常用的LQG，H2 ，H∞ , l2 ,混合H2/H∞和混合l1/H∞，都是將所有控制目標，轉變成一個閉環傳遞函式矩陣的加權範數的最最佳化問題。一般的多目標控制指的是時域性能和頻域性能的混合，比如從H2和H∞性能到區域極點配置，漸進跟蹤或調節，調整時間，飽和度約束。
基本介紹
- 中文名：多目標控制
- 外文名：Multi-target control
- 類別：控制科學與工程
- 方法：H2控制等
- 問題：Lyapunov函式的閉環性能指標問題
- 實現方法：變權重係數法等
基本概念,多目標控制的發展,模型及實現方法,變權重係數法,並列選擇法,選擇排序法,
基本概念
控制系統的多目標最佳化設計一直是人們致力研究的課題，比如常用的LQG，H2 ，H∞ , l2 ,混合H2/H∞和混合l1/H∞，都是將所有控制目標，轉變成一個閉環傳遞函式矩陣的加權範數的最最佳化問題。H2和H∞是一種頻域設計方法，不能直接包括時域性能。最近l2最佳化問題得到了廣泛的研究，它考慮的是將信號的幅值限制在一定範圍內，這是一種表述時域性能的方法，但是不能用於頻率性能的設計問題。
顯然，通常不同的設計性能是矛盾的，比如抑制不同特點的干擾(白噪聲，有界能量，持續激勵);好的輸入跟蹤能力;輸出峰值有界;好的魯棒性。這些性能通常不能表示在一個範數當中。自然就會想到混合的多目標最佳化控制。
一般的多目標控制指的是時域性能和頻域性能的混合，比如從H2和H∞性能到區域極點配置，漸進跟蹤或調節，調整時間，飽和度約束。下面是一些常用的方法和目標:
- H∞性能比較適合於具有模型不確定的魯棒控制和表達頻域性能指標: 頻寬，低頻增益和衰減度。
- H2性能用於處理隨機測量噪聲和任意的擾動。
- 時域約束用來調整暫態回響和峰值，比如脈衝回響峰值，階躍回響的超調量和控制輸入的峰值。
- 極點配置對避免快速的動態回響和高頻增益抑制非常有用，這樣有利於數字實現。
上個世紀90年代初，隨著求解凸最佳化算法的內點法的出現，LMI再一次受到了控制屆的關注。許多控制問題都可以轉化為一個LMIs的可行解問題，或一個具有LMIs約束的凸最佳化問題。之後很多學者將基於LMI的方法運用到多目標控制問題中去，Chilali和Gahinet提出了用LMIs解決具有區域極點約束的H∞控制問題。 Schere:等對一些常用的集成方法進行蒐集和概括，總結了很多可以用LMI描述的多目標控制方法，並首先提出了多通道的思想進行多目標控制的框架。在這些方法的基礎上，Masubuchi等抽象並簡化了許多控制方法的LMIs表達式。
多目標控制的發展
在過去的十年里，許多單目標控制問題己經得到廣泛的關注。幾個重要的控制器集成問題可以表述成最佳化問題，如比較常用的LQG、H2、l2等理論為我們提供了一些基本集成工具。這些理論背後潛在的前提是將所有的控制目標轉變成一個閉環傳遞函式矩陣的加權範數的最最佳化問題。
LQG特別適用於要保證存在干擾的閉環系統穩定性並滿足性能指標的控制問題。儘管如此，如果LQG用於具有觀察器或者Kalman濾波器的系統時，就不能保證魯棒性的裕度。這就發展了H∞控制理論，它能很好地處理魯棒穩定性問題:當存在系統不確定時能保證閉環系統穩定。對具有結構不確定的系統，H∞控制可以進化成μ集成。μ集成己經成功的運用到許多實際控制問題中。然而，H∞控制是一種頻率控制方法，不能直接包括時域性能。最近，l1最佳化控制問題得到廣泛的研究，它考慮的是將信號幅值限制在一定範圍內，這是一個表述時域性能的方法，但是不用於有頻率性能的控制問題(如H2範數約束)。
顯然，通常不同的設計性能都是相互矛盾的，比如同時抑制不同特點的干擾(白噪聲，有界能量，持續激勵);好的輸入跟蹤能力;輸出峰值有界。這些性能通常都不能表示成一個範數形式。故很自然就會用到混合的多目標控制。一般的多目標控制指的是時域和頻域性能的混合，比如從H2和H∞性能到區域極點配置，漸近跟蹤或調節，調整時間，飽和度約束。下面為一些常用的性能指標和目標：
- H∞性能比較適合於具有模型不確定的魯棒控制和表達頻域性能指標: 頻寬，低頻增益和衰減度。
- H2性能用於處理隨機測量噪聲和任意的擾動。
- 時域約束用來調整暫態回響和峰值，比如脈衝回響峰值，階躍回響的超調量和控制輸入的峰值。
- 極點配置對避免快速的動態回響和高頻增益抑制非常有用，這樣有利於數字實現。
多目標H2 /H∞控制問題，是用於指定關於一個Lyapunov函式的閉環性能指標的問題。它以損失一些保守性來滿足期望的性能。其優點是控制器設計可以轉換成一個凸最佳化問題。許多相同的技術用於狀態反饋控制問題，被證明在滿足設計目標時是非常有價值的。
研究人員提出了一個全新的基於LMI的一般混合HZI戈輸出反饋集成問題。這個工作終於可以從狀態反饋情況‘23’通過一些比較簡單的控制器參數轉換實現輸出反饋控制的問題。儘管這些經過參數變換後的控制問題比狀態反饋要複雜，但它提供了一種相等對稱性概念，可以將輸出反饋的性能參數轉換到LMIs表達式中。
20世紀90年代初，隨著求解凸最佳化問題的內點法的提出，LMI再一次受到控制界的關注，並被套用到系統的控制的各個領域中。許多控制問題可以轉化為一個LMIs的可行性問題，或者是一個具有LMIs約束的凸最佳化問題。1998年，Matlab推出了求解LMI問題的LMI工具箱，從而使得人們更加方面和有效地處理、求解LMIs，進一步推動了LMI方法在系統和控制領域的套用。之後很多學者將基於LMI的方法運用到各種多目標控制系統中去。Chilali和Gahinet提出了用LMIs解決具有區域極點約束的凡控制問題。Schere等對一些常用的集成方法進行蒐集和概括，總結很多關於多目標控制方法的LMIs分析和集成，並首先提出來用多通道的思想進行多目標控制的框架。在這些方法基礎上，Masubuchi等抽象並簡化了許多控制方法的LMIs表達式。
1999年D'Andrea 提出了離散的廣義L2(GL2)分析框架，這個方法可以解決具有元素一元素有界不確定性系統的魯棒穩定控制問題。基於LMI方法，廣義l2控制能得到全局最優解，並且是可數字跟蹤的。GL2控制框架在解決魯棒穩定性問題上的保守性比H∞控制小。 wang J.在原有文獻基礎上包含了GL2控制目標，擴展了多目標控制，並將它套用車輛懸掛系統，效果不錯。
模型及實現方法
在實際的電力系統中，往往根據某一目標設計控制器，該控制器的效果是令人滿意的。但是在實際中，往往會遇到要求系統的多個控制目標都達到最佳化的情況，而事實上如果同時針對這些目標設計控制器，其控制效果可能不令人滿意甚至控制器之間可能會互相起到負作用，例如根據SVC的電壓穩定和阻尼功率振盪兩個目標分別設計出來的控制器在實際運行中，其作用是相互起著負作用的;UPFC中針對不同的控制功能設計出來的的不同控制器之間也存在著相互的影響，這種影響甚至會影響到系統的閉環穩定性。在分散式潮流控制器中，也必然存在著這樣的問題。然而，其要想得到廣泛的套用，這種涉及到多個控制器間相互協調的問題就首先要得到解決。這就是多目標控制所涉及到的問題了。
在很多時候，多目標最佳化問題中不同子目標不是相互促進的，要想提高某一目標的性能，則其它另一個或多個目標的性能就會得到降低，目標子函式之間存在矛盾。因此只能在這些相互衝突的子目標之間尋求一種平衡，使得各個不同的子目標在條件滿足的情況下都儘可能得到最佳化。這就決定了多目標最佳化與單目標最佳化問題在本質上的區別。
如果一個多目標問題存在著最優解，那這個最優解一定是Pareto最優解，並且Pareto最優解也只能由這些最優解組成而不再包含其他的解。也就是說，Pareto最優解是多目標最佳化問題合理解的集合。
多目標最佳化問題的Pareto最優解其實質上是一系列解的集合，在實際情況中，往往是根據具體的情況以及經驗從Pareto最優解中選出一個解來作為最優問題的解。因此，在多目標問題的求解過程中，最重要的就是求得Pareto最優解。
通過以上分析可以知道，遺傳算法被可以套用到的多目標問題求解中，這是因為遺傳算法的運算對象是種群，其包含了多個個體，這就可以和多目標問題中的多個子目標相關聯。在多目標問題的求解中，其滿意解也是包含了多個參數的一個集合，這也與種群中個體的概念可以聯繫起來。以下將介紹幾種多目標求解的方法。
變權重係數法
根據多目標問題中子目標函式在最終整體性能中所起影響的大小進行評估，也就是按照各個不同的目標函式在整體性能中的重要程度來設定其權重值。該方法可以將多目標最優解求解的問題轉化為求解整體評價函式最優解的問題。採用該方法可以得到多目標問題的Pareto解。
並列選擇法
這種方法將全體個體按照目標函式的數目均等的分為不同的子群體，對於不同的子群體採用不同的目標函式，在這些不同的群體中針對其不同的目標函式獨立進行選擇運算，將選擇出來的一些適應度比較高的個體組成一個新的子群體，然後將這些子群體合為一個新的群體。在這個群體中進行交叉和變異運算，生成下一代的群體。以上的過程不斷循環，可以求取多目標最最佳化問題中的Pareto最優解。
選擇排序法
在這種方法中，群體進化中產生的Pareto最優個體不一定對應著多目標最佳化問題的Pareto最優解。選擇排序法就是利用與Pareto最優解的符合程度來確定種群中個體的先後次序，然後以這個序列作為參考，進行種群的進化，以最大的機率將Pareto最優個體遺傳到下一代中。
