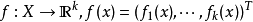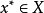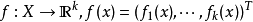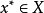方法簡介
多目標最佳化(又稱多目標規劃、向量最佳化、多準則最佳化、多目標最佳化或帕累托最佳化)是多目標決策的一個領域,它涉及到多目標函式的最佳化問題,同時也是多目標最佳化問題。多目標最佳化已經套用到科學的許多領域,包括工程、經濟和物流,在兩個或更多衝突的目標之間存在取捨時,需要採取最優決策。在購買汽車時儘量減少成本,同時最大限度地發揮舒適度,同時最大限度地降低汽車的油耗和污染物排放,是多目標最佳化問題的例子,涉及兩個和三個目標。在實際問題上,可以有三個以上的目標。 對於一個非平凡的多目標最佳化問題,沒有單一的解決方案同時最佳化每一個目標。在這種情況下,目標函式是相互衝突的,並且存在一個(可能是無窮數)的帕累托最優解。一個解決方案稱為非劣解,帕累托最優,帕累托有效或非劣效性,如果沒有一個目標函式在價值上可以得到改進,而沒有降低其他客觀值。如果沒有額外的主觀偏好信息,所有帕累托最優解都被認為是相當好的(因為向量不能完全有序)。研究人員從不同的角度對多目標最佳化問題進行了研究,在建立和解決這些問題時,存在著不同的解決方法和目標。其目的是尋找一組代表性的帕累托最優解,並/或量化在滿足不同目標的權衡取捨,以及/或找到一個滿足人類決策者主觀偏好的單一解決方案。
提出和形式
多目標規劃是指含有多個目標函式的規劃問題。在數學中,多目標規劃法可以寫成下面的形式:
其中k≥2,是指目標函式的個數,集合X是一組可行的決策向量集。可行集通常由一些約束函式定義。此外,向量值目標函式通常被定義為:
。
元素
被稱為可行的解決方案或可行的決定。對可行解x*得到的向量
稱為目標向量或者是結果。
在多目標最佳化中,通常沒有一種可行的解決方案,使所有目標函式同時最小化。因此,應注意帕累托最優解決方案,即在任何目標中都不能改進的解決方案,而不損害至少一個目標。
標準型特點
與線性規劃相比,多目標規劃標準型的特點在於:
1、偏差列向量 Y − 、Y + 。Y − 、Y + 分別為負、正偏差列向量,各有 m個元素 Y − 、y + 。…與 ,…,(m是約束方程的個數)。負偏差變數的經濟含義為當實際值小於目標值時,實際值與目標值的偏差為負偏差,正偏差變數的經濟含義與之恰恰相反。
2、價值係數行向量c。c的元素最多不超過 2m個,由目標優先權等級 Pi和目標優先權係數η組成,即 c = (c1,c2…,c2m)=(),在多目標規劃的目標函式中,出現的變數只能是偏差變數。也就是說,列向量 y以正偏差變數和負偏差變數為元素。目標優先權等級 Pi既不是變數,也不是常數,它只是說明不同目標實現的先後順序,這種優先等級的確定一般是由企業決策部門根據企業具體情況及各目標的輕重緩急加以確定的。而目標優先權係數,則說明同一優先權目標相互之間的比例關係。
基本解法
多目標規劃的解法主要有單純形法和圖解法。圖解法一般只適用於兩個決策變數的情形。單純形法對於求解多目標規劃有普遍意義。
由於多目標最佳化問題通常存在多個
帕累托最優解,解決這類問題的方法並不像傳統的單目標最佳化問題那樣簡單。因此,不同的研究者對“解決多目標最佳化問題”這一術語進行了不同的界定。本節概述了其中一些和使用它們的上下文。許多方法將原問題與多目標轉化為一個單一目標最佳化問題。這被稱為一個標量化問題。如果標量化做得很好,可以保證所獲得的解的帕累托最優性。 求解多目標最佳化問題,有時被理解為逼近或計算所有或有代表性的帕累托最優解集。 在強調決策的過程中,解決多目標最佳化問題的目標是支持決策者根據自己的主觀偏好尋找最優的帕累托最優解。 基本假設是,必須確定一個解決問題的辦法,以便在實踐中加以實施。在這裡,一個人類決策者扮演著重要的角色。預計dm將成為問題領域的專家。 最喜歡的結果可以用不同的哲學來找到。多目標最佳化方法可分為四類。在所謂的“不偏好”方法中,預計不會有dm,但在沒有偏好信息的情況下,確定了一個中立的折衷解決方案。其他類都是所謂的先驗、後驗和互動方法,它們都以不同的方式從dm中涉及偏好信息。 在先驗的方法中,首先從dm中提出偏好信息,然後找到最滿意這些偏好的解決方案。在後驗方法中,首先發現了一組代表性的帕累托最優解,然後再選擇其中一組。在互動方法中,允許決策器疊代搜尋最優先的解決方案。在互動方法的每一次疊代中,dm都得到了帕累托最優解,並描述了解決方案的改進。然後在生成新的帕累托最佳化解的同時考慮決策者給出的信息,以便在下一次疊代中學習。這樣,dm就能了解他/她的願望的可行性,並能集中精力解決他/她所感興趣的解決方案。每當他/她想要的時候,dm就可以停止搜尋。下面幾節中給出了四個類中不同方法的更多信息和示例。
目標優先權排序 P1,P2,…,PN給出了單純形疊代過程中實現目標的順序。在實現某一優先權目標後,應依順序考慮一個優先權能否實現。但是,不能為實現較低目標而使較高級目標的實現受到影響。
主要套用領域
多目標規劃的概念是 1961年由美國數學家查爾斯和庫柏首先提出的。至今有些理論問題尚在探討之中,套用範圍還不如線性規劃廣泛。在資源分配、計畫編制、生產調度等方面有一定的’套用。但是,作為一種決策方法,多目標規劃的套用前景還是很樂觀的。企業決策者掌握和運用這種方法將有助於提高管理和決策水平。
經濟學
在經濟學中,許多問題涉及多個目標,同時限制了可實現哪些目標的組合。例如,消費者對各種商品的需求是由最大化這些商品所產生的公用事業的過程決定的,受制於基於可用於這些商品的收入以及這些商品的價格的限制。這種約束允許更多的一件商品只能在犧牲另外一種商品的情況下被購買;因此,各種目標(每個商品的消費更多是首選)是相互矛盾的。分析這種問題的常用方法是使用表示偏好的無差異曲線圖和預算約束,表示消費者面臨的權衡。
另一個例子涉及生產可能性的前沿,它規定了具有一定數量的各種資源的社會可以生產各種類型的商品的組合。邊界規定了社會所面臨的權衡 - 如果社會充分利用資源,只有以犧牲另外一個好成本為代價才能產生更多的一個好處。一個社會必須採取一些過程來選擇邊界的可能性。
巨觀經濟決策是需要多目標最佳化的一個環境。通常,中央銀行必須為貨幣政策選擇平衡競爭目標的態度 - 低通貨膨脹率,低失業率,低餘額的貿易逆差等。為此,中央銀行使用經濟模型,定量描述各種因果關係在經濟中它在貨幣政策的各種可能的情況下反覆模擬模型,以便獲得各種感興趣變數的可能預測結果的選單。那么原則上,它可以使用總目標函式對預測結果的替代集合進行評估,儘管實際上中央銀行使用非定量的,基於判斷的流程來排列替代方案並做出政策選擇。
財經
在財務方面,一個常見的問題是當有兩個衝突的目標時,選擇一個投資組合 - 希望將投資組合回報的預期價值儘可能高,並且希望有風險,往往以投資組合回報的標準差來衡量,儘可能低。這個問題通常由一個圖表示,其中有效邊界顯示了可用的風險和預期回報的最佳組合,其中無差異曲線顯示投資者對各種風險預期回報組合的偏好。最佳化期權價值(第一時刻)的功能和投資組合回報的標準差(第二中心時刻的平方根)的問題稱為兩時決策模型。
最佳控制
在工程和經濟學方面,許多問題涉及多個目標,不能被描述為更好或更好的;相反,每個目標都有一個理想的目標值,並且希望儘可能接近每個目標的期望值。例如,能源系統通常在性能和成本之間取捨,或者可能想要調整火箭的燃料使用和方向,使其在指定的地點和指定的時間到達;或者可能想進行公開市場操作,以使通貨膨脹率和失業率都儘可能接近他們所期望的價值。
通常,這些問題經受線性等式約束,從而阻止所有目標同時完全滿足,特別是當可控變數的數量小於目標數量以及隨機衝擊的存在產生不確定性時。通常使用多目標二次目標函式,其中與客觀物體的距離與其理想值的二次方成正相關的成本。由於這些問題通常涉及在各個時間點調整受控變數和/或評估各個時間點的目標,因此採用跨期最佳化技術。
最佳設計
使用現代建模,仿真和最佳化技術可以大大提高產品和工藝設計。最佳設計的關鍵問題在於衡量設計的好壞。在尋找最佳設計之前,重要的是確定對設計總體價值最有價值的特性。良好的設計通常涉及多個標準/目標,如資本成本/投資,運營成本,利潤,質量和/或產品回收率,效率,工藝安全性,操作時間等。
例如,在設計造紙廠時,可以減少造紙廠投入的資金,同時提高紙張的質量。如果造紙廠的設計是由大量存儲量定義的,紙質量由質量參數定義,則造紙廠最佳設計的問題可以包括以下目標:i)將這些質量參數的預期變化從其最小化名義值,ii)最小化預期的休息時間,以及iii)最小化存儲量的投資成本。在這裡,最大塔數是設計變數。造紙廠最佳化設計的這個例子是使用的模型的簡化。工程系統中也實現了多目標設計最佳化 - 例如。納米CMOS半導體的設計、太陽能灌溉系統設計、砂模系統最佳化、發動機設計、最佳化感測器部署、和最優控制器設計。
流程最佳化
化學工程越來越多地採用多目標最佳化。 2009年,Fiandaca和Fraga採用多目標通用算法(MOGA)來最佳化變壓吸附過程(循環分離過程)。設計問題涉及氮回收和氮純度的雙重最大化。結果提供了帕累托前沿的良好近似,在目標之間具有可接受的權衡。
2010年,Sendín等解決了食品熱處理的多目標問題。他們用非線性動力學模型處理了兩個案例研究(雙目標和三目標問題),並採用了加權Tchebycheff和Normal Boundary Intersection方法組合的混合方法。新型混合方法能夠構建食物熱處理的帕累托最優集。
2013年,Ganesan等進行甲烷二氧化碳重整和部分氧化的多目標最佳化。目標函式是甲烷轉化率,一氧化碳選擇性和氫氣與一氧化碳的比例。 Ganesan使用正交邊界交叉(NBI)方法結合兩種基於群的技術(重力搜尋算法(GSA)和粒子群最佳化(PSO))來解決這個問題。
涉及化學提取和生物乙醇生產工藝的套用提出了類似的多目標問題,得到了解決。
在2013年,Abakarov等人提出了一種替代技術來解決食品工程中出現的多目標最佳化問題。使用聚合函式方法,自適應隨機搜尋算法和懲罰函式方法來計算非主導或帕累托最優解的初始集合。同時使用分析層次過程和表格方法來選擇滲透脫水過程的非主導解決方案的計運算元集中的最佳替代方案。
無線電資源管理
無線電資源管理的目的是滿足蜂窩網路用戶請求的數據速率。主要資源是時間間隔,頻率塊和發射功率。每個用戶都有其自己的目標功能,例如,可以表示數據速率,延遲和能量效率的某種組合。這些目標是矛盾的,因為頻率資源非常稀缺,因此需要緊密的空間頻率重用,如果不能正確控制,則會引起巨大的用戶間干擾。多用戶MIMO技術現在用於通過自適應預編碼來減少干擾。網路運營商希望既能獲得極高的覆蓋率和高數據速率,因此運營商也希望找到一種以適當的主觀方式平衡總網路數據吞吐量和用戶公平性的帕累托最優解決方案。
無線電資源管理通常通過標量化來解決;也就是說,選擇一個嘗試平衡吞吐量和用戶公平性的網路效用函式。效用函式的選擇對結果單目標最佳化問題的計算複雜度有很大的影響。例如,加權和速率的共同效用給出了NP-hard問題,複雜度隨著用戶數量呈指數級數增長,而加權最大最小公平效用導致了僅具有多項式縮放的準凸最佳化問題,用戶數量。
電力系統
通過交換系統要素之間的功能聯繫,重新配置是可以提高配電系統運行性能的最重要措施之一。通過配電系統的重構,在其定義方面的最佳化問題是一個歷史性的單一客觀現象。