多元線性模型(multiple linear model)是數理統計的一個重要分支,在一元線性模型中研究的指標Y是一元隨機變數,影響指標Y的因素可以有多個因素,這些因素中可以有定性因子,也可以有定量因子,如果我們研究的指標Y是P元隨機變數,影響指標y的因素有多個因素,這就是多元模型的問題。
基本介紹
- 中文名:多元線性模型
- 外文名:multiple linear model
- 所屬學科:數學
- 所屬領域:數理統計
- 相關概念:一元線性模型、隨機變數等
基本介紹


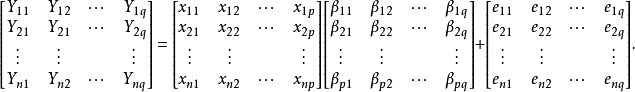

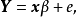





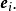


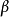

多元線性模型的參數估計
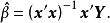

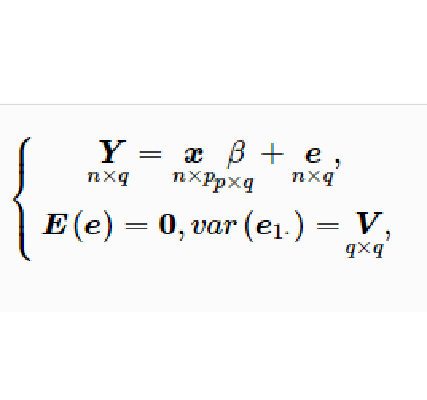
多元線性模型(multiple linear model)是數理統計的一個重要分支,在一元線性模型中研究的指標Y是一元隨機變數,影響指標Y的因素可以有多個因素,這些因素中可以有定性因子,也可以有定量因子,如果我們研究的指標Y是P元隨機變數,影響指標y的因素有多個因素,這就是多元模型的問題。


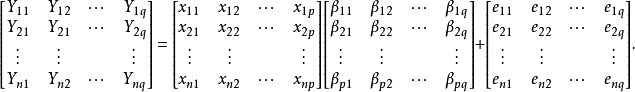

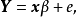





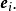


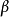


多元線性回歸模型,(multivariable linear regression model )在實際經濟問題中,一個變數往往受到多個變數的影響。例如,家庭消費支出,除了受家庭可支配收入的影響外,還...
多元線性模型(multiple linear model)是數理統計的一個重要分支,在一元線性模型中研究的指標Y是一元隨機變數,影響指標Y的因素可以有多個因素,這些因素中可以有定性...
多元線性回歸與一元線性回歸類似,可以用最小二乘法估計模型參數,也需對模型及模型參數進行統計檢驗[2] 。選擇合適的自變數是正確進行多元回歸預測的前提之一,多元...
線性模型是一類統計模型的總稱,製作方法是用一定的流程將各個環節連線起來,包括線性回歸模型、方差分析模型,套用於生物、醫學、經濟、管理。...
研究一個因變數、與兩個或兩個以上自變數的回歸。亦稱為多元線性回歸,是反映一種現象或事物的數量依多種現象或事物的數量的變動而相應地變動的規律。建立多個變數...
多元回歸分析(Multiple Regression Analysis)是指在相關變數中將一個變數視為因變數,其他一個或多個變數視為自變數,建立多個變數之間線性或非線性數學模型數量關係式...
上述的各種方法可以看成廣義多元分析的內容,在有些方法中,如加上正態性的假定,就可以討論一些更深入的問題,例如線性模型中有關線性假設檢驗的問題,在正態的假定下...
多元回歸模型是用來進行回歸分析的數學模型(含相關假設),其中只含有一個回歸變數的回歸模型稱為一元回歸模型,否則稱為多元回歸模型。...
多元性回歸模型與一元線性回歸模型一樣,在得到參數的最小二乘法的估計值之後,也需要進行必要的檢驗與評價,以決定模型是否可以套用。...
包括3類:①多元方差分析、多元回歸分析和協方差分析,稱為線性模型方法,用以研究確定的自變數與因變數之間的關係;②判別函式分析和聚類分析,用以研究對事物的分類;...
(這反過來又應當由多個相關的因變數預測的多元線性回歸區別,而不是一個單一的標量變數。)線上性回歸中,數據使用線性預測函式來建模,並且未知的模型參數也是通過數據...
回歸模型(regression model)對統計關係進行定量描述的一種數學模型。如多元線性回歸的數學模型可以表示為y=β0+β1*x+εi,式中,β0,β1,…,βp是p+1個待...
這種函式是一個或多個稱為回歸係數的模型參數的線性組合。只有一個自變數的情況稱為簡單回歸,大於一個自變數情況的叫做多元回歸。(這反過來又應當由多個相關的因...
不過,在大量運用多元邏輯 回歸的研究中往往忽視了另一個相當重要的問題,即模型自變數之間可能存在的多重共線性干擾。與其他多元回歸方法一樣,Logistic回歸模型也對...
《分層線性模型》是由社會科學文獻出版社於2007-1所出版的圖書,本書作者是Raudenbush,S.W.,本書譯者是郭志剛。...
《多元統計分析:模型、案例及SPSS套用》由經濟科學出版社於2010年3月正式出版發行,本教材的適用對象主要是財經類院校的統計專業本科生和經濟與管理類學科的碩士研究...
均平穩,而且平穩序列的線性組合仍然是平穩的,所以殘差序列 為平穩序列:使用...多元非平穩序列之間能否建立動態回歸模型,關鍵在於它們之間是否具有協整關係,因此要...
這是最常用的模型,稱為多重線性回歸或多元線性回歸。用樣本估計線性回歸模型中未知常數的方法也很多,經典的方法為最小二乘法,它的理論較為完善,此法較適用於回歸...
