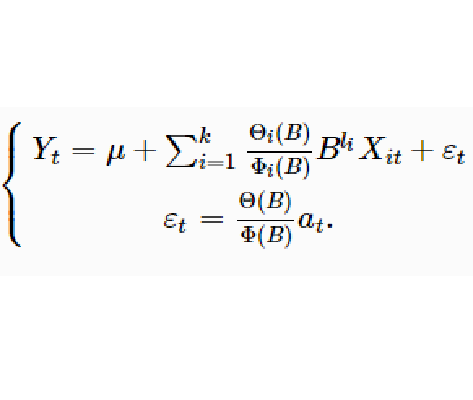基本介紹 實際中很多序列的變化規律都會受到其他序列的影響,比如在研究居民的人均消費序列時,由於消費會受收入的影響,如果能把收入也納入研究範圍,就能得到更精確的消費模型,這就涉及
多元時間序列分析 。1976年,Cox和Jenkins就採用天然氣的輸入速率作為輸入變數,研究二氧化碳的輸出濃度.這就將時間序列分析由一元推廣到了多元的場合。但從技術上講,當時要求輸入序列和輸出序列都是平穩的,顯然這是非常苛刻的,進而限制了多元時間序列分析的套用。1987年Engle和Cranger提出了
協整理論 ,在此理論下,並不要求回響序列和輸入序列都平穩,只要求它們的回歸殘差序列平穩,這極大地促進了多元時間序列的發展,它實際上是將
多元回歸分析 和
時間序列 分析 有機地結合在一起,有效地提高了預測精度。
重要概念 動態回歸模型 1976年Cox和Jenkins採用帶輸入變數的ARIMA模型,為平穩多元序列建模,該模型的構造思想是:假設回響序列
和輸人變數序列(即自變數序列)
均平穩,首先構建回響序列和輸入變數序列的回歸模型:
式中,
為第i個輸入變數的自回歸係數多項式,
為第i個輸入變數的移動平均係數多項式,
為第i個輸入變數的延遲階數,
為回歸殘差序列。
值得注意的是:回歸模型不僅僅是
關於
的回歸,也可以是關於
的延遲變數的回歸。
因為{
}和
均平穩,而且平穩序列的線性組合仍然是平穩的,所以殘差序列
為平穩序列:
使用ARMA模型繼續提供殘差序列{‘}中的相關信息,最終得到的模型為
該模型稱為
動態回歸模型 ,簡記為ARIMAX,式中
為殘差序列自回歸係數多項式,
為殘差序列移動平均係數多項式,
為零均值白噪聲序列。
在ARIMAX模型中,如果平穩性條件不滿足,就容易產生虛假回歸的問題。我們考慮一元線性回歸模型
,為了檢驗模型的顯著性,就需要對擬合模型進行檢驗:
假定回響序列和輸入變數序列相互獨立,理論上,檢驗結果應該接受原假設
,如檢驗結果為拒絕
,那么我們就接受了一個本不應該成立的回歸模型,從而犯了第一類錯誤(棄真錯誤)。由於樣本的隨機性,故棄真錯誤會一直存在,我們可採用顯著性水平
控制棄真錯誤的機率
。
通常情況下,我們採用t統計量進行參數顯著性檢驗:
。當{
}和{
}都平穩時,該統計量服從自由度為樣本容量的t分布,從而有
當{
}和{
}不平穩時,隨機模擬的結果顯示,檢驗統計量
不服從t分布,這時t統計量的樣本方差遠遠大於t分布的方差,如果仍採用t分布的臨界值進行檢驗,拒絕原假設的機率就會大大增加,這樣導致我們無法控制棄真錯誤,容易接受本不該成立的回歸模型,這種現象稱為虛假回歸。
協整 在現實生活中我們會發現,有些序列自身的變化雖然是非平穩的,但是序列與序列之間卻具有非常密切地長期均衡關係,為了有效地衡量序列之間是否具有長期均衡關係,Engle和Granger 於1987 年提出了協整概念。
關於協整的含義,我們可以藉助一個通俗的例子來加以解釋。假設一男一女在舞廳里跳交誼舞,如果記錄下男士和女士的活動軌跡,就得到了兩條沒有明顯線性趨勢的軌跡。雖然這兩條軌跡都是非穩定的,但是卻有一個關係是始終存在的:這兩條軌跡始終受到某種規律的限制與聯結(如遵照的舞曲)而保持同步。這種二者之間一起變化的關係可看作協整關係。聯繫到兩個時間序列,儘管兩個序列都是非平穩的,但它們的某種線性組合卻可能是平穩的。例如消費
和國民收人
都是單位根過程,但變數
卻是平穩的。在這種情況下,我們稱
和
是協整的,稱
為協整參數。
“協整”概念與經濟學的“均衡”概念有本質上的聯繫。協整揭示了變數之間的一種長期穩定的均衡關係,是均衡關係在統計上的表述,因此在實證檢驗中用來判斷變數間存在均衡關係的證據。比如,兩個變數,雖然它們具有各自的長期波動規律,但如果它們是協整的,則它們之間存在著一個長期穩定的比例關係;反之,如果兩個變數具有各自的長期波動規律,但它們不是協整的,則它們之間就不存在著一個長期穩定的比例關係。從圖形上直觀地講,圖1顯示1966年至1993年間中國實際國民收入GNP的對數序列和實際消費C的對數序列的變化情況,兩者很可能存在協整關係,而圖2顯示的兩序列則隨時間變化相距越來越遠,不可能存在均衡關係。
圖1 GDP與消費的關係 圖2 結合
單整 概念,可得到關於協整的正式定義:如果序列
都是d階單整,存在一個向量
,使得
,其中b>0,
,則認為序列
是(d,b)階協整,記為
為協整向量。例如:國民收入時間序列
為1階單整序列,居民消費時間序列
也為1階單整序列,如果二者的線性組合
構成的新序列為0階單整序列,於是認為序列
與
是(1,1)階協整。可見,如果兩個變數都是單整變數,只有當它們的單整階數相同時,才可能協整。
EG檢驗 多元非平穩序列之間能否建立動態回歸模型,關鍵在於它們之間是否具有協整關係 ,因此要對多元非平穩序列建模,必須先進行協整檢驗 ,也稱Engle-Granger,簡稱EG檢驗。由於自然界中絕大多數序列之間不具有協整關係,所以EG檢驗的假設條件如下確定:
由於協整關係主要是通過考察回歸殘差的平穩性確定,所以上述假設條件等價於:
EG檢驗 也稱為EG兩步法 ,它遵循如下兩個步驟:
步驟一 :建立回響序列與輸入序列之間的回歸模型:
我們主要是採用單位根檢驗的方法來考察回歸殘差序列的平穩性,EG檢驗原理與計算公式的DF檢驗原理及計算公式相同,但是蒙特卡洛模擬的結果顯示,它們的臨界值略有不同,EG檢驗的臨界值不僅與位移項、趨勢項等因素有關,而且還與同歸模型中非平穩變數的個數相關,Mackinnon提供了EG檢驗的臨界值表,並將EG檢驗的臨界值表與ADF檢驗的臨界值表結合在一起。當非平穩序列的個數大於等於2時,對應的就是EG檢驗。








































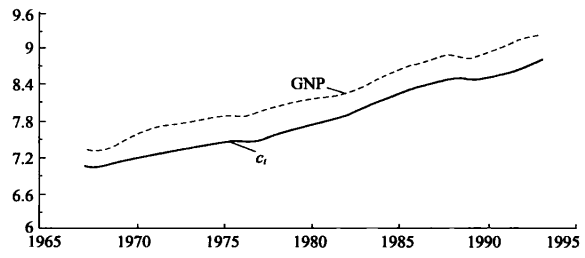 圖1 GDP與消費的關係
圖1 GDP與消費的關係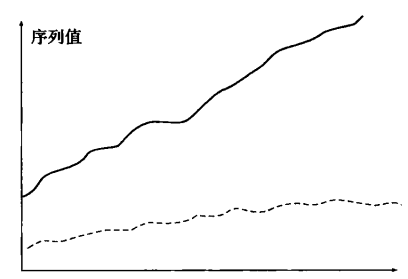 圖2
圖2