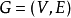基本介紹
- 中文名:多主體最佳化系統
- 外文名:multiagent optimization system
組合最佳化,群集智慧型,背包問題,圖著色問題,旅行推銷員問題,
組合最佳化
組合最最佳化,在套用數學和理論計算機科學的領域中,組合最佳化是在一個有限的對象集中找出最優對象的一類課題。在很多組合最佳化的問題中,窮舉搜尋/枚舉法是不可行的。組合最佳化的問題的特徵是可行解的集是離散或者可以簡化到離散的,並且目標是找到最優解。常見的例子有旅行商問題和最小生成樹。二維的例子,比如服裝廠做衣服,衣服分成很多塊,這些塊需要從布料上切下來。怎么切,剩下的廢布料最少?三維的例子,如集裝最佳化。
組合最佳化的難處,主要是加進來拓撲分析,不同的拓撲形態下,不同部分的約束關係便不同,算法也就要調整。如果給定一個拓撲形態,組合最佳化往往就退化成一個整數最佳化的問題了。
群集智慧型
典型的群集智慧型系統由一群簡單的主體構成,每個主體和其它主體以及它們的環境作局部的互動。儘管通常沒有集中控制機制來指示這些主體如何協作,但這些簡單的局部互動行為通常能湧現出複雜的全局行為。當前主要的幾種群集智慧型方法包括蟻群算法和粒子群最佳化。
背包問題
背包問題(Knapsack problem)是一種組合最佳化的NP完全問題。問題可以描述為:給定一組物品,每種物品都有自己的重量和價格,在限定的總重量內,我們如何選擇,才能使得物品的總價格最高。問題的名稱來源於如何選擇最合適的物品放置於給定背包中。
圖著色問題
圖著色問題(英語:Graph Coloring Problem,簡稱GCP),又稱著色問題,是最著名的NP-完全問題之一。
旅行推銷員問題
旅行推銷員問題(最短路徑問題)(英語:Travelling salesman problem,TSP)是這樣一個問題:給定一系列城市和每對城市之間的距離,求解訪問每一座城市一次並回到起始城市的最短迴路。它是組合最佳化中的一個NP困難問題,在運籌學和理論計算機科學中非常重要。
TSP是旅行購買者問題與車輛路徑問題的一種特殊情況。
問題在1930年首次被形式化,並且是在最最佳化中研究最深入的問題之一。許多最佳化方法都用它作為一個基準。儘管問題在計算上很困難,但已經有了大量的啟發式和精確方法,因此可以完全求解城市數量上萬的實例,並且甚至能在誤差1%範圍內估計上百萬個城市的問題。