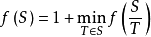基本介紹
- 中文名：圖著色問題
- 外文名：Graph Coloring Problem, GCP
- 又稱：著色問題
- 屬於：最著名的NP-完全問題之一。
簡介,路線著色問題,算法,算法描述,暫存器分配技術,
簡介
圖的m-著色最佳化問題——若一個圖最少需要m種顏色才能使圖中任意相鄰的2個頂點著不同顏色，則稱這個數m為該圖的色數。求一個圖的最小色數m的問題稱為m-著色最佳化問題。
路線著色問題
G是一個有限有向圖並且G的每個頂點的出度都是k。G的一個同步著色滿足以下兩個條件：
1)G的每個頂點有且只有一條出邊被染成了1到k之間的某種顏色；
2)G的每個頂點都對應一種走法，不管你從哪裡出發，按該走法走，最後都結束在該頂點。
有向圖G存在同步著色的必要條件是G是強連通而且是非周期的。一個有向圖是非周期的是指該圖中包含的所有環的長度沒有大於1的公約數。路線著色定理這兩個條件(強連通和是非周期)也是充分的。也就是說,有向圖G存在同步著色若且唯若G是強連通而且是非周期的。
道路著色問題（Road Coloring Problem）是圖論中最著名的猜想之一。通俗的說，這個猜想認為，可以繪製一張“萬能地圖”，指導人們到達某一目的地，不管他們原來在什麼位置。這個猜想最近被以色列數學家艾夫拉漢· 特雷特曼(Avraham Trahtman)在2007年9月證明。
以色列人也為特雷特曼取得的成就感到無比的驕傲。特拉維夫電視台中斷了正常的節目播放，以第一時間發布了這一重大訊息，連中東其他國家的主流媒體也作了大篇幅的相關報導。
得知特雷特曼解決這一難題的訊息後，多年從事路線著色問題研究的加拿大數學家喬爾·弗里德曼說，“路線著色問題的解決令數學共同體非常興奮。”讀過特雷特曼論文的中國數學家和語言學家周海中教授認為，特雷特曼的數學知識非常淵博，解題方法十分巧妙，這一謎題得到破解，無疑是數學史上的一個華彩樂章。
算法
點著色問題有簡單的時間複雜度為O(3^n)的算法，即設f(S)表示集合的色數，則
。
算法描述
color[n]存儲n個頂點的著色方案，可以選擇的顏色為1到m。
當t=1時，對當前第t個頂點開始著色：若t>n，則已求得一個解，輸出著色方案即可。否則，依次對頂點t著色1-m， 若t與所有其它相鄰頂點無顏色衝突，則繼續為下一頂點著色；否則，回溯，測試下一顏色。
#include<stdio.h> int color[100];bool ok(int k,int c[][100])//判斷頂點k的著色是否發生衝突{ int i,j; for(i=1;i<k;i++) { if(c[k][i]==1&&color[i]==color[k]) return false; } return true;} void graphcolor(int n,int m,int c[][100]){ int i,k; for(i=1;i<=n;i++) color[i]=0; k=1; while(k>=1) { color[k]=color[k]+1; while(color[k]<=m) if(ok(k,c)) break; else color[k]=color[k]+1;//搜尋下一個顏色 if(color[k]<=m&&k==n) { for(i=1;i<=n;i++) printf("%d",color[i]); printf("\n"); } else if(color[k]<=m&&k<n) k=k+1;//處理下一個頂點 else { color[k]=0; k=k-1;//回溯 } }}void main(){ int i,j,n,m; int c[100][100];//存儲n個頂點的無向圖的數組 printf("輸入頂點數n和著色數m:\n"); scanf("%d%d",&n,&m); printf("輸入無向圖的鄰接矩陣:\n"); for(i=1;i<=n;i++) for(j=1;j<=n;j++) scanf("%d",&c[i][j]); printf("著色所有可能的解:\n"); graphcolor(n,m,c);}暫存器分配技術
利用相交圖（interference graph）來表示程式變數的生命期是否相交，將暫存器分配給變數的問題，可近似地看成是給相交圖著色：相交圖中，相交的節點不能著同一顏色；每一種顏色對應一個暫存器。Chaitin等人最早提出了基於圖著色的暫存器分配方法其著色思路採用了Kempe的著色方法，即，任意一個鄰居節點數目少於k的節點，都能夠被k著色。判斷一個圖是否能夠被k(k>=3)種顏色著色，即k著色問題，被Karp證明是一個NP-complete問題。
但是，暫存器分配不僅僅是圖著色的問題。當暫存器數目不足以分配某些變數時，就必須將這些變數溢出到記憶體中，該過程成為spill。最小化溢出代價的問題，也是一個NP-complete問題。如果簡化該問題——假設所有溢出代價相等，那么最小化溢出代價的問題，等價於k著色問題，仍然是NP-complete問題。
此外，若兩個變數的生命期僅因為在同一個拷貝指令中而相鄰，那么，通過將這兩個變數分配到同一個暫存器，就可以消除該拷貝指令，成為coalescing。這個方向的努力在Chaitin的文章以後的1/4個世紀，成為推動暫存器分配的主要動力之一，湧現出了包括aggressive coalescing,conservative coalescing和optimistic coalescing。但是，將兩個變數分配到同一個暫存器，等價於將這兩個變數合併成同一個變數，生命期合併，因而會加劇相交圖的聚簇現象，降低相交圖的可著色性。Bouchez等人證明了coalescing問題都是NP-complete的。
為降低相交圖的聚簇現象，提高相交圖的可著色性，可通過將變數拷貝給一個臨時變數，並將以後對該變數的使用替換成對該臨時變數的使用，從而將一變數的生命期分解成兩個變數的生命期，稱為live range splitting。顯然，這是一個與coalescing的作用相反的過程。Bouchez等人考慮了該方法的複雜度。
此外，暫存器分配還需要考慮暫存器別名(aliasing)和預著色(pre-coloring)的問題。暫存器別名是指，在某些體系結構中，一個暫存器的賦值可能會影響到另外一個暫存器。比如，在x86中，對AX暫存器的賦值，會影響AL和AH暫存器。預著色是指，某些變數必須被分配到特定的暫存器。比如，許多體系結構會採用特定暫存器來傳遞函式參數。
