外映射半徑是複平面上的某個圓盤的半徑。
基本介紹
- 中文名:外映射半徑
- 外文名:outer mapping radius
- 適用範圍:數理科學
- 學科:數學
簡介
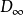
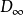
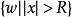
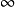
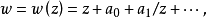
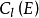
內映射半徑
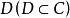
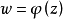
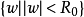
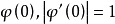
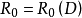
性質
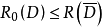
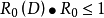
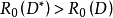
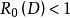
外映射半徑是複平面上的某個圓盤的半徑。
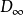
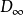
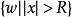
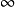
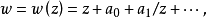
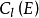
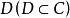
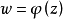
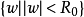
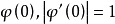
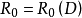
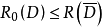
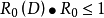
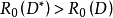
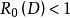
外映射半徑是複平面上的某個圓盤的半徑。...... 外映射半徑是複平面上的某個圓盤的半徑。設E 是複平面 C 上的有界連續統, 是開集 C\E 中那個無界的分支,...
若共形映射ω=φ(z)將D映成{ω||ω|<R0},並使φ(0),|φ'(0)|=1,則稱R0=R0(D)為D關於0的內映射半徑。中文名 內映射半徑 外文名 inner mapping...
貝爾特拉米映射羅氏幾何的基本性質 編輯 因為羅氏平面可以看成半徑為純虛數的球面,所以,利用貝爾特拉米映射可以導出羅氏幾何的基本性質。設球面上點 M 點坐標為 的對應...
單射半徑是對完備黎曼流形的一個刻畫,是使指數映射為微分同胚的最大半徑。...... 單射半徑是對完備黎曼流形的一個刻畫,是使指數映射為微分同胚的最大半徑。...
可擴映射(expansive map)是一類重要的動力系統。設(M,d)是一個度量空間,f:M...設x0∈R,r>0,則稱集合{x|x∈R,ρ(x,x0)<r}為以x0為中心,r為半徑...
紋理映射(Texture Mapping)是將紋理空間中的紋理像素映射到螢幕空間中的像素的...S : (u, v) --> (x', y', z') --- S-映射如半徑為R的球的S-...
證明,如果A : X→ Y是巴拿赫空間之間的連續線性滿射,那么A就是一個開映射...因此,存在一個開球B(c, r),其中心為c,半徑r > 0,包含在A(kU)的閉包內...
反響映射(英語:reverberation mapping)是天體物理學中通過觀測活動星系核中寬發射線對於連續譜的回響來測量寬發射線區(英語:broad emission-line region, BLR)半徑的...
