貝爾特拉米映射是球面到平面的一種特殊映射。這個映射是貝爾特拉米 (Beltraim,E.)在研究羅氏幾何時首先提出來的，稱為貝爾特拉米映射。
基本介紹
- 中文名：貝爾特拉米映射
- 外文名：Beltrami mapping
- 適用範圍：數理科學
- 提出者：貝爾特拉米
簡介,羅氏幾何的基本性質,
簡介
貝爾特拉米映射是球面到平面的一種特殊映射。
在空間直角坐標系中，取一個半徑為 a 的球面，設球心 C 在 z 軸上，且球面與平面 xOy 切於坐標原點。對於球面上任一點 M，過 C，M 作直線交於 xOy 面於一點 m，稱 m 為球麵點 M 經過球心投射而得到的對應點，並規定球面上在一條直徑上點的對應平面上的同一點。這樣就得到球面到平面的一個映射（如圖）。
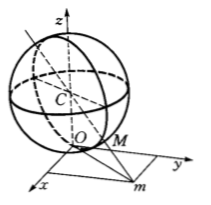圖1.這個映射是貝爾特拉米 (Beltraim,E.)在研究羅氏幾何時首先提出來的，稱為貝爾特拉米映射。
羅氏幾何的基本性質
因為羅氏平面可以看成半徑為純虛數的球面，所以，利用貝爾特拉米映射可以導出羅氏幾何的基本性質。設球面上點 M 點坐標為
的對應點 m 在 xOy 面上，記為 m(x,y)。又設
，這裡 ρ 稱為羅氏曲率半徑，由球面上弧長的微分式
可以導出羅氏平面弧長的公式
